
目录
文章难度:★★☆☆☆
使用负债比率、平均营收成长率、平均税后净利率、股价营收比和股价研发比等五项财务指标筛选强势成长股
阅读建议:本文资料来源皆来自TEJ API的公司财务资料库,如果对Python的Dataframe操作不是很熟悉的读者,可以先行阅读【新手上路(六)】- 财务数据捞取中的程式码,能更好理解本文中的操作流程。
肯尼斯.费雪( kenneth L. Fisher)是费雪投资公司(Fisher Investments)的创办人兼总裁,他的父亲菲利普.费雪(Philip A. Fisher)是美国体质投资(Qualitative Investment)的代表;华伦.巴菲特(Warren Buffett)特别指出菲利普.费雪是他两个主要投资灵感的启发者之一【另一个当然是班杰明.葛拉汉(Benjamin Graham)】,由此可见肯尼斯.费雪的投资家学非常渊源。
肯尼斯.费雪认为一支完美的超级强势股应有下列特性一,利用自有资金创造未来,长期平均成长率约为15%-20%。二,未来长期平均税后获利率高于5%。三,股价/营收比为0.75或更低。在选股方面,肯尼斯.费雪考虑两个项因素:一,是股价/营收比,二,是股价/研发费用比,且有明确的准则。
a.避开PSR超过1.5的股票,任何PSR大于3的公司决不要碰。
b.积极寻找PSR低于0.75的超级公司。
c.任何超级公司的PSR涨到3至6之间时,要卖出持股。
别买PRR高于15的公司,PRR低的超级公司多的是。
寻找PRR介于5至10的超级公司,PRR低于5倍的公司不多见。
1. 负债比率低于35%
2. 最近5年平均营收成长率≧15%
3. 最近5年平均税后净利率≧5%
4. 股价营收比(PSR)≦1.5
5. 股价/研发费用比(PRR) ≦15
此外,由于该策略没有明确的出场时机点,但由于台湾的公司月营收都于每个月初时公布,因此我们以一个月为周期进行筛选,同时对投资组合进行再平衡调整。
本文使用Windows OS并以jupyter作为编辑器
import tejapi as tej import pandas as pd import numpy as np import datetime import matplotlib.pyplot as plt tej.ApiConfig.api_key = 'Your Key'
plt.rcParams['font.sans-serif'] = ['Taipei Sans TC Beta']
IFRS财务会计科目说明档(TWN/AIACC)
调整股价(日)-除权息调整(TWN/APRCD1)
证券属性资料表(TWN/ANPRCSTD)
IFRS以合并为主财务(单季)-全部产业Ⅳ(TWN/AIFINQ)
上市(柜)月营收盈余(TWN/ASALE)
首先我们从「IFRS财务会计科目说明档」搜寻所需的会计科目代号,再从「IFRS以合并为主财务(单季)-全部产业Ⅳ」资料库下载所有上市柜公司的负债比率、税后净利率和研发费用,至于营收成长率及股价营收比我们另外从「上市(柜)月营收盈余」资料库抓取。
financial_name = tej.get('TWN/AIACC', chinese_column_name=True, paginate=True) #找寻所需的会计科目
financial_dict = ['负债比率', '税后净利率', '研发费用']
a = []
for i in financial_dict:
a.append(financial_name[financial_name['中文全称'].str.contains(i)]['会计科目'].mode().to_list())
a
使用pd.Series.str.contains再取众数的方式得知R505为负债比率、R108为税后净利率、3368为研发费用。
使用公司代号及特定的会计科目代号下载所需的财务和月营收资料。
#上市柜公司代号
code = tej.get('TWN/ANPRCSTD', mdate={'lt':'2022-10-14'}, chinese_column_name=True, paginate=True)
all_code = code[(code['证券种类名称'] == '普通股') & (code['上市别'].isin(['TSE', 'OTC']))]['证券码'].to_list()
#下载近十年的财务数据
financial_data = tej.get('TWN/AIFINQ',
coid=all_code,
mdate={'gt': '2012-01-01', 'lt':'2022-10-14'},
acc_code=a,
chinese_column_name=True,
paginate=True)
financial_data = financial_data.reset_index(drop=True)
#下载近十年的月营收数据
revenue_data = tej.get('TWN/ASALE',
coid=all_code,
mdate={'gt': '2011-12-31', 'lt':'2022-10-14'},
opts={'columns': ['coid', 'mdate', 'd0001']},
chinese_column_name=True,
paginate=True)
revenue_data.rename(columns={'年月': '年/月'}, inplace=True)
revenue_data['公司'] = revenue_data['公司'].astype(int)
revenue_data = revenue_data.astype({'年/月':'datetime64[ns]'})
股价由于资料量极大,因此每隔一个月下载一批资料再用pd.concat合并,最后串接成一笔三百万的资料集。
m = pd.date_range('2011-12-31', '2022-11-01', freq='1M', inclusive='both').to_list()
price = pd.DataFrame()
for i in range(1, len(m)):
price = pd.concat([price, tej.get('TWN/APRCD1',
coid=all_code,
mdate={'gt': m[i-1], 'lt':m[i]},
opts={'columns': ['coid', 'mdate', 'close_adj', 'mv']},
chinese_column_name=True,
paginate=True)])
price = price.reset_index(drop=True)
price = price.rename(columns={'证券代码':'公司', '年月日':'年/月'})
price['公司'] = price['公司'].astype(int)
price = price.astype({'年/月':'datetime64[ns]'})
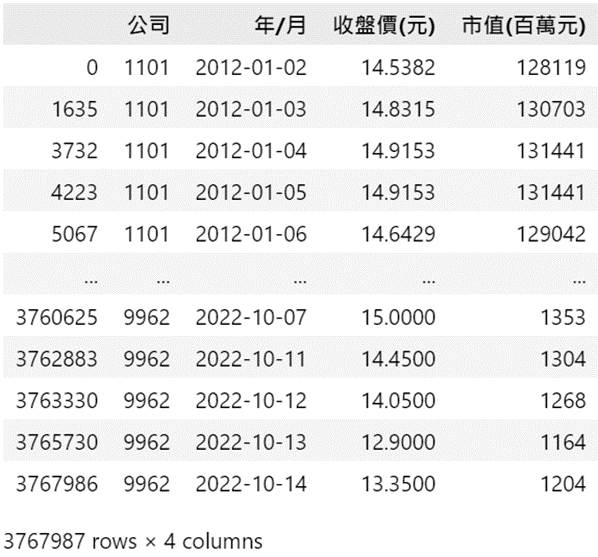
进一步整理财务数据,将R505、R108、3368分别转为中文的会计名称,并使用pd.pivot_table进行格式转置以方便之后进一步的合并。
financial_data1 = financial_data.copy() financial_data1['数值'] = financial_data1['数值'].astype(float)
financial_data1['会计科目'] = financial_data1['会计科目'].map({'R505':'负债比率', #会计科目改名
'R108':'税后净利率',
'3368':'研发费用'})
financial_data1 = financial_data1.pivot_table(index=['公司', '年/月'], columns='会计科目', values='数值').reset_index() #格式转置
financial_data1['公司'] = financial_data1['公司'].astype(int)
financial_data1 = financial_data1.astype({'年/月':'datetime64[ns]'})
financial_data1 = financial_data1.fillna(0)
financial_data1
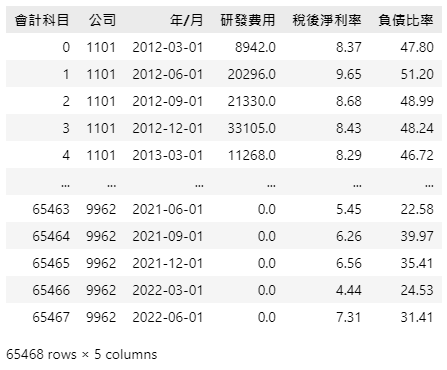
使用pd.merge_asof将财务数据、月营收和股价合并成每月为单位的资料集。
financial_data1 = pd.merge_asof(revenue_data.sort_values('年/月'), financial_data1.sort_values('年/月'), on='年/月', by='公司', direction='backward').sort_values(['公司', '年/月'])
financial_data1 = pd.merge_asof(financial_data1.sort_values('年/月'), price.sort_values('年/月'), on='年/月', by='公司', direction='nearest').sort_values(['公司', '年/月'])
financial_data1
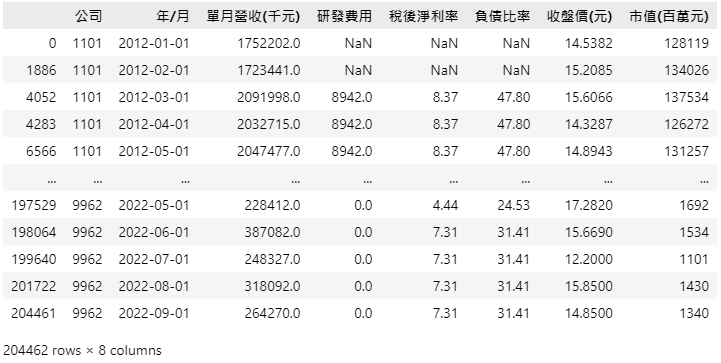
计算策略所需的五年平均营收年成长率、股价营收比和股价研发比。
financial_data1['营收年成长率'] = financial_data1['单月营收(千元)'] / financial_data1['单月营收(千元)'].shift(12)
financial_data1['平均5年营收成长率'] = financial_data1.groupby('公司')['营收年成长率'].transform(lambda x: x.rolling(60).mean())
financial_data1['平均5年税后净利率'] = financial_data1.groupby('公司')['税后净利率'].transform(lambda x: x.rolling(60).mean())
financial_data1['近一年营收总合'] = financial_data1.groupby('公司')['单月营收(千元)'].transform(lambda x: x.rolling(12).sum()/1000)
financial_data1['股价营收比'] = financial_data1['市值(百万元)'] / financial_data1['近一年营收总合']
financial_data1['近一年研发总合'] = financial_data1.groupby('公司')['研发费用'].transform(lambda x: x.rolling(12).sum()/1000)
financial_data1['股价研发比'] = financial_data1['市值(百万元)'] / financial_data1['近一年研发总合']
financial_data2 = financial_data1[['公司', '年/月', '负债比率', '收盘价(元)', '平均5年营收成长率', '平均5年税后净利率', '股价营收比', '股价研发比']].reset_index(drop=True)
financial_data2
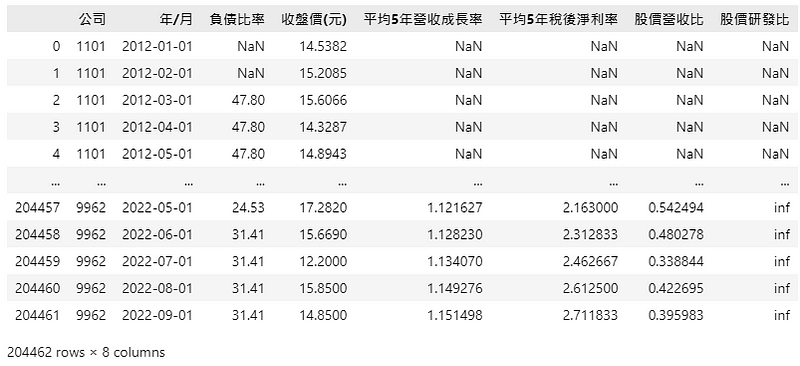
我们将筛选器组成一个function方便之后进一步的参数优化比较,并简单计算年化报酬率、年化标准差和年化夏普指标。
def condition(df, n1, n2, n3, n4, n5):
price_T = price.pivot_table(index='年/月', columns='公司', values='收盘价(元)')
target_stock = df[(df['负债比率'] < n1) & (df['平均5年营收成长率'] >= n2) & (df['平均5年税后净利率'] >= n3) & (df['股价营收比'] <= n4) & (df['股价研发比'] <= n5)]
target_Q = list(target_stock.groupby('年/月')[['公司', '年/月', '收盘价(元)']])
ret, daily_ret = [], []
for i in range(len(target_Q)):
daily_ret.append(price_T.loc[target_Q[i][1].iloc[0]['年/月']:target_Q[i][1].iloc[0]['年/月']+pd.DateOffset(months=1), target_Q[i][1]['公司'].to_list()])
ret.append(price_T.loc[target_Q[i][1].iloc[0]['年/月']:target_Q[i][1].iloc[0]['年/月']+pd.DateOffset(months=1), target_Q[i][1]['公司'].to_list()].pct_change().mean(axis=1))
ret_table = pd.concat(ret)
ret_table = pd.DataFrame(columns=['投组日报酬'], data=ret_table).dropna()
ret_table['投组累积报酬'] = (ret_table['投组日报酬'] +1).cumprod()
ret_table.reset_index(inplace=True)
print('年化报酬率:',"%6.3f" % (ret_table['投组日报酬'].mean()*252))
print('年化标准差:',"%6.3f" % (ret_table['投组日报酬'].std()*np.sqrt(252)))
print('年化夏普:',"%6.4f" % (ret_table['投组日报酬'].mean()*252 / (ret_table['投组日报酬'].std()*np.sqrt(252))))
return ret_table, target_stock[['公司', '年/月', '收盘价(元)']], daily_ret
设定(n1)负债比率35%、(n2)近5年平均营收成长率≧15%、(n3)近5年平均税后净利率≧5%、(n4)股价营收比(PSR)≦1.5、(n5)股价/研发费用比(PRR) ≦15,可以看出在三年的投资期间最终有75.7%的累计报酬率,年化报酬率达36%(投组实际持股天数少于三年时间,因此年化后数值较高),夏普比率也有1.3869的水准。注:无风险利率设为0%,无计入手续费与交易税。
ret_table, target_stock, daily_ret = condition(financial_data1, 35, 15, 5, 1.5, 15) ret_table
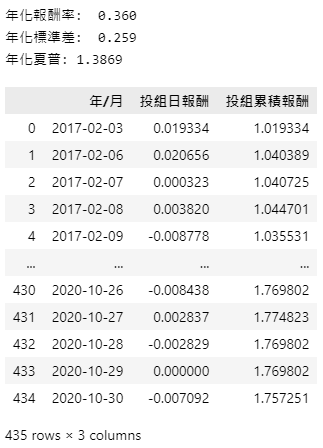
为了更直观的审视策略绩效,我们另外下载大盘报酬指数Y9997作为基准,来比较看看该策略是否能赢过单纯投资大盘。
y9997 = tej.get('TWN/APRCD1',
coid='y9997',
mdate={'gt': '2017-02-01', 'lt':'2022-10-14'},
opts={'columns': ['coid', 'mdate', 'close_adj']},
chinese_column_name=True,
paginate=True)
y9997['基准日报酬'] = y9997['收盘价(元)'].pct_change()
y9997['基准累积报酬'] = (y9997['基准日报酬']+1).cumprod()
y9997.rename(columns={'年月日':'年/月'}, inplace=True)
y9997 = y9997.astype({'年/月':'datetime64[ns]'})
从图中我们可以看出,初期找到不错的标的可以快速超越大盘,但在2020年末股市V型反弹后就找不太优秀的成长股,主要原因可能是资金大量的涌入容易在短时间内将股价与营收表现脱节,导致股价营收比这项比率的设定,限缩了股市暴涨行情中能找到的标的;此外近一年无研发费用的公司将导致股价研发比呈现无限大,使其被股价研发比<15的条件所淘汰,最终在2020年末以后不再有适合的标的。
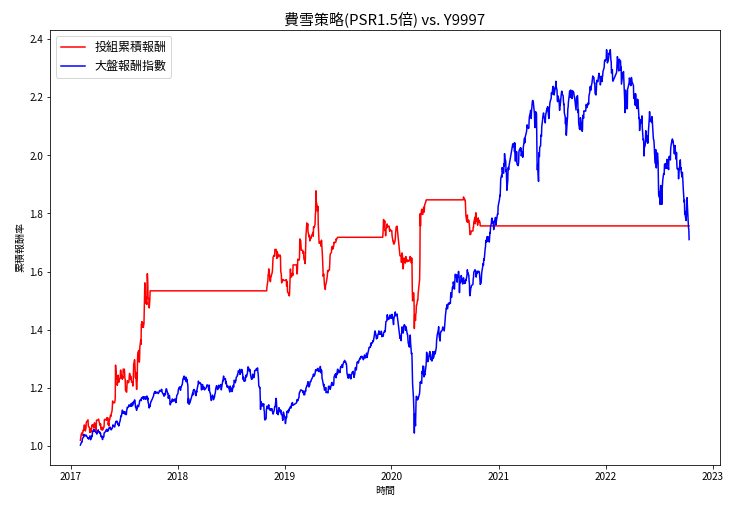
为了测试该策略能否更显著赢过大盘,我们对之前的参数进一步放宽,特别是股价营收比这项限制,从1.5倍放宽到2倍的区间。可以看到放宽后虽然标准差有所增加,但随之而来的报酬率更加显著,让整体的夏普比率从1.3869提高了47%上升到2.0448的水平。
ret_table2, target_stock2, daily_ret2 = condition(financial_data1, 35, 15, 5, 2, 15)
ret_table2
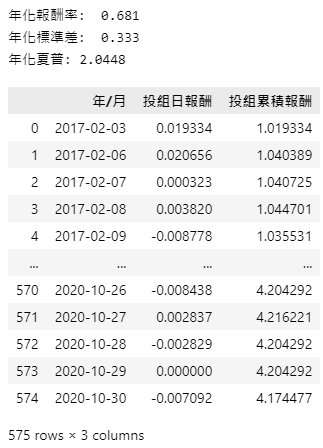
从下表能看出由于该策略所找寻的是成长型股票,对比同期间的Y9997基准有著至少两倍的差距,标的特点在于爆发力高且注重未来展望,因此整体来说BETA值也比较大,所以在面对新冠肺炎的股市暴跌时,可以看出投组的回撤也比同期间的大盘来的严重。
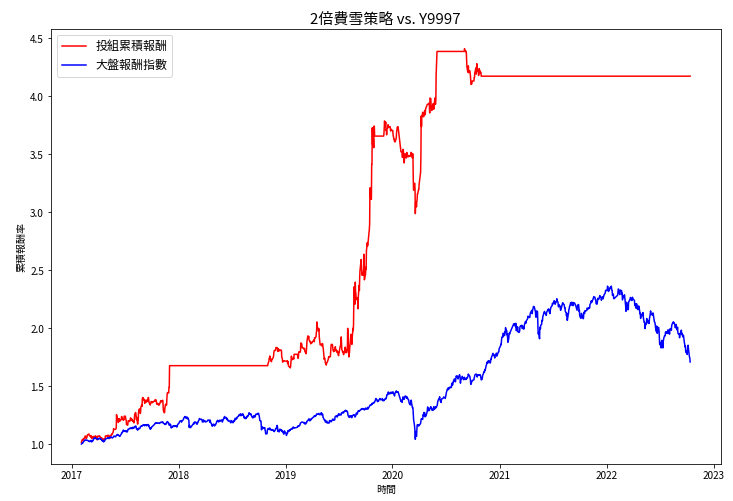
而我们也能发现主要报酬皆来自2019年中至年末这段时间。从程式码里面去找这段期间,发现只有6538仓和这支个股,若拆开来单算它的报酬率就高达83%,对投组整体的贡献十分惊人。
(pd.concat(daily_ret2)['2019-08-01': '2019-12-01'].pct_change()+1).cumprod()
总体而言,肯尼斯.费雪这支策略核心在于以股价营收比(PSR)找寻被低估的成长型股票,而公司自身则需要有持续投入研发费用,并在低负债比率的情况下,提高营收成长率并维持一定水平的税后净利率。
不过原策略的PSR 0.75倍~1.5倍对台股而言过于严格,导致在股市大反弹期间PSR太低的限制会无法找到标的,而我们在放宽至PSR 2倍后也成功找到仓和的起涨点,将投组整个报酬率拉升不少。要注意的是该策略只有提供选股的逻辑,并没有出场或停损的相关设定,若使用者要参照该策略组建投组,建议要多参考其他指标作为出场点和停损的依据。
此外本策略无计算手续费以及交易税等成本,提醒使用者在参考本策略时须多加注意。
最后,还是要再次提醒本文所提及之标的仅供说明使用,不代表任何金融商品之推荐或建议。因此,若读者对于建置策略、绩效回测、研究实证等相关议题有兴趣,欢迎选购 TEJ E Shop中的方案,具有齐全的资料库,就能轻易的完成各种检定。

电子报订阅