配对交易

Jan 11 2022

本文重点概要

文章难度：★★★☆☆
阅读建议：配对交易是一种利用两、三种具有对冲效果的资产组合，消除大部分市场风险，获得市场中性的效果，并设定进出场条件，在资产的价差序列中产生进出场讯号，获得既能避险又能盈利的策略。先前有介绍过定态性，而本文进一步将时间序列的理论应用在配对交易上，若想了解更多理论推导，可参考金融科技实战。

前言

当市场资金过度泛滥时，投资人为了规避系统性风险，常透过资产配置的方式同时建立多空部位，来消除大部份市场风险，获得稳定报酬。而本文挑选长荣与阳明做为配对交易的股票对，并以单根检定确定两档价差存在定态性，即确认长荣与阳明具有共整合关系，从而在价差偏离时，买进被低估的股票，卖出被高估的股票，并在价差修正时，反向平仓，赚取价差。

编辑环境及模组需求

本文使用 Windows OS 并以 Jupyter Notebook 作为编辑器

# 基本功能
import pandas as pd
import numpy as np
from arch.unitroot import ADF
import statsmodels.api as sm
# 绘图
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['Microsoft JhengHei']
plt.rcParams['axes.unicode_minus'] = False
# TEJ API
import tejapi
tejapi.ApiConfig.api_key = 'Your Key'

资料库使用

报酬率资讯表：上市(柜)股价报酬(日)-资料代码为(TWN/EWPRCD2)。

资料处理

从 TEJ资料库汇入长荣与阳明的股价报酬率。

# 汇入资料
stock = tejapi.get('TWN/EWPRCD2',
                   coid = ['2603','2609'],
                   mdate= {'gte': '2019-06-01','lte':'2021-06-30'},
                   opts={'columns':['coid','mdate','roia']},
                   chinese_column_name=True,paginate=True)
stock = stock.pivot(index='日期', columns='证券码', values='日报酬率(%)')
stock.columns = ['2603 长荣','2609 阳明']
stock = stock * 0.01
stock.tail(6)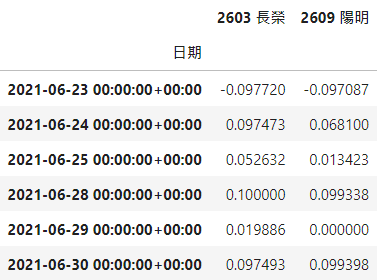

共整合检定

Step 1. 股票日报酬率序列有定态性

从下图看出两档日报酬率都在0附近上下波动，可以确定两档日报酬率序列存在定态性。

# 长荣与阳明 日报酬率的时序图
fig = plt.figure(figsize = (15,8))
ax = fig.add_subplot()
ax.plot(stock['2603 长荣'] ,linewidth=2, alpha=1)
ax.plot(stock['2609 阳明'] ,linewidth=2, alpha=0.7)
ax.axhline(0,color = 'black')
ax.set_title('长荣与阳明 日报酬率的时序图' ,fontsize=20 ,fontweight='bold')
ax.legend(['2603 长荣','2609 阳明'],loc='best')
ax.set_ylabel('报酬率', fontsize=12,rotation=0)
ax.grid(axis='y')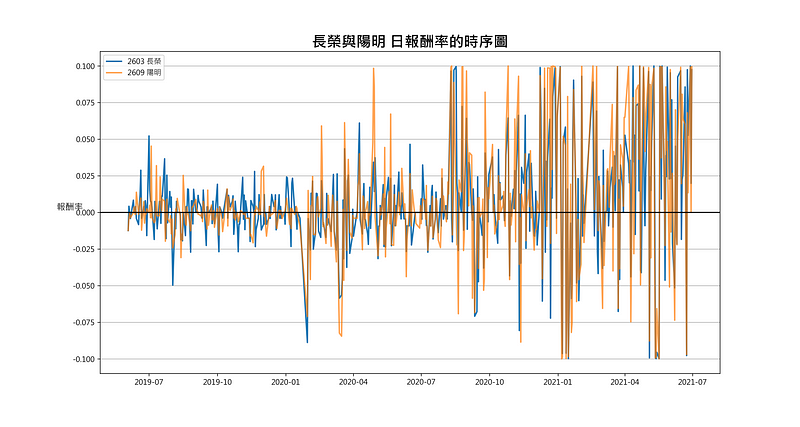

Step 2. 股票对的价差

先将回测期间分成形成期与交易期，我们在计算交易期的价差序列时，为了避免前视偏误，我们使用形成期价差序列的线性回归而得的 alpha系数值与 beta系数值，计算交易期的价差序列。

# 价差
def CointegrationSpread(df,formStart,formEnd,tradeStart,tradeEnd):
    formX = df[(df.index >= formStart) & (df.index <= formEnd)]['2603 长荣']
    formY = df[(df.index >= formStart) & (df.index <= formEnd)]['2609 阳明']
    tradeX = df[(df.index >= tradeStart) & (df.index <= tradeEnd)]['2603 长荣']
    tradeY = df[(df.index >= tradeStart) & (df.index <= tradeEnd)]['2609 阳明']
    results = sm.OLS(formY,sm.add_constant(formX)).fit()
    spread = tradeY - results.params[0] - results.params[1] * tradeX
    return spread
Spread_2020_10_12 = CointegrationSpread(stock,'2019-06-01','2020-06-30','2020-10-01','2020-12-31')
Spread_2021_01_03 = CointegrationSpread(stock,'2020-01-01','2020-12-31','2021-01-01','2021-03-30')
# 对两档股价的价差序列做定态性检定
adfSpread = ADF(Spread_2021_10_12, trend='n')
print(adfSpread.summary().as_text())

由下图可知在1%显著性水平下，我们可以拒绝虚无假设，说明 2021_10_12价差序列是定态的，即长荣与阳明的日报酬率序列具有共整合关系。

mu = np.mean(Spread_2020_10_12)
sd = np.std(Spread_20201012)

我们计算形成期价差序列的 μ均值与 σ标准差，获得交易期进出场的条件门槛值。设定 μ±1.5σ和 μ±0.2σ为开仓与平仓的临界值，而 μ±2.5σ.

。同时我们可以发现形成期价差序列都没有触及 μ±2.5σ临界值。

建立配对交易策略

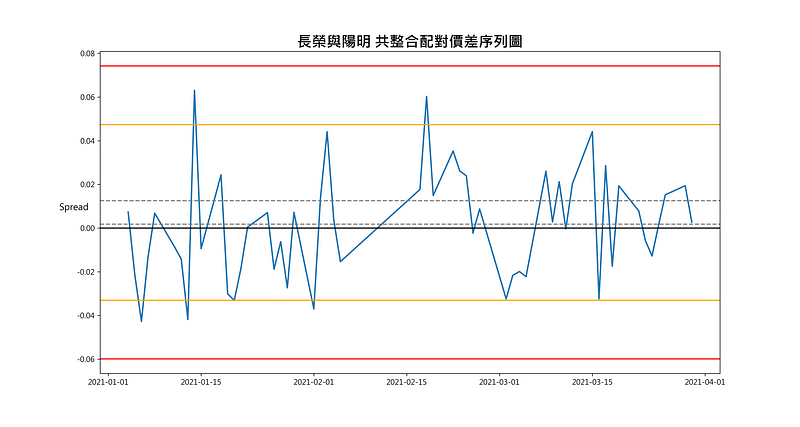
我们根据开仓平仓点制定交易策略，

当价差上穿 μ+1.5σ时，做空配对股票，反向建仓（卖出阳明；买进长荣）。
当价差下穿 μ+0.2σ时，做多配对股票，反向平仓。
当价差上穿 μ−1.5σ时，做多配对股票，反向建仓（买进阳明；卖出长荣）。
当价差上穿 μ−0.2σ时，做空配对股票，反向平仓。
当价差突破 μ±2.5σ时，即时平仓。

Spread_2021_01_03 = Spread_2021_01_03.to_frame()
Spread_2021_01_03.columns = ['价差']Spread_2021_01_03['开仓平仓区间'] = 
    pd.cut(Spread_2021_01_03['价差'] ,
           (float('-inf') ,mu-2.5*sd ,mu-1.5*sd ,mu-0.2*sd ,
            mu+0.2*sd ,mu+1.5*sd ,mu+2.5*sd ,float('inf')) ,labels=False)-3Spread_2021_01_03['交易讯号'] = 
    np.select([(Spread_2021_01_03['开仓平仓区间'].shift() == 1) &
               (Spread_2021_01_03['开仓平仓区间'] == 2),
               (Spread_2021_01_03['开仓平仓区间'].shift() == 1) &
               (Spread_2021_01_03['开仓平仓区间'] == 0),
               (Spread_2021_01_03['开仓平仓区间'].shift() == 2) &
               (Spread_2021_01_03['开仓平仓区间'] == 3),
               (Spread_2021_01_03['开仓平仓区间'].shift() == -1) &
               (Spread_2021_01_03['开仓平仓区间'] == -2),
               (Spread_2021_01_03['开仓平仓区间'].shift() == -1) &
               (Spread_2021_01_03['开仓平仓区间'] == 0),
               (Spread_2021_01_03['开仓平仓区间'].shift() == -2) &
               (Spread_2021_01_03['开仓平仓区间'] == -3)],
              [-2,2,3,1,-1,-3],default = 0)position = [Spread_2021_01_03['交易讯号'][0]]
ns = len(Spread_2021_01_03['交易讯号'])Spread_2021_01_03['仓位情况'] = pd.Series(position,index=Spread_2021_01_03.index)
Spread_2021_01_03['仓位情况'] = Spread_2021_01_03['仓位情况'].shift() # 隔天开盘才进场Spread_2021_01_03 = Spread_2021_01_03.join(stock)
Spread_2021_01_03['策略报酬率'] = 
    np.select([Spread_2021_01_03['仓位情况'] == 1,
               Spread_2021_01_03['仓位情况'] == 0,
               Spread_2021_01_03['仓位情况'] == -1],
              [Spread_2021_01_03['2609 阳明'] * -1 + Spread_2021_01_03['2603 长荣'] * 1,
               0,
               Spread_2021_01_03['2609 阳明'] * 1 + Spread_2021_01_03['2603 长荣'] * -1], default=np.nan)Spread_2021_01_03['累积报酬率'] = (Spread_2021_01_03['策略报酬率'] + 1).cumprod() -1
Spread_2021_01_03.head(10)

我们完成上述策略，并将策略的累积报酬率与最大回档呈现在下图。

结论

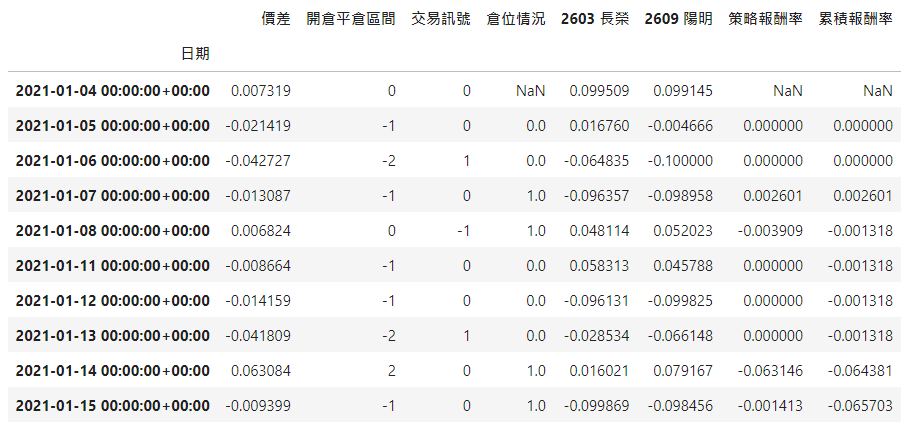
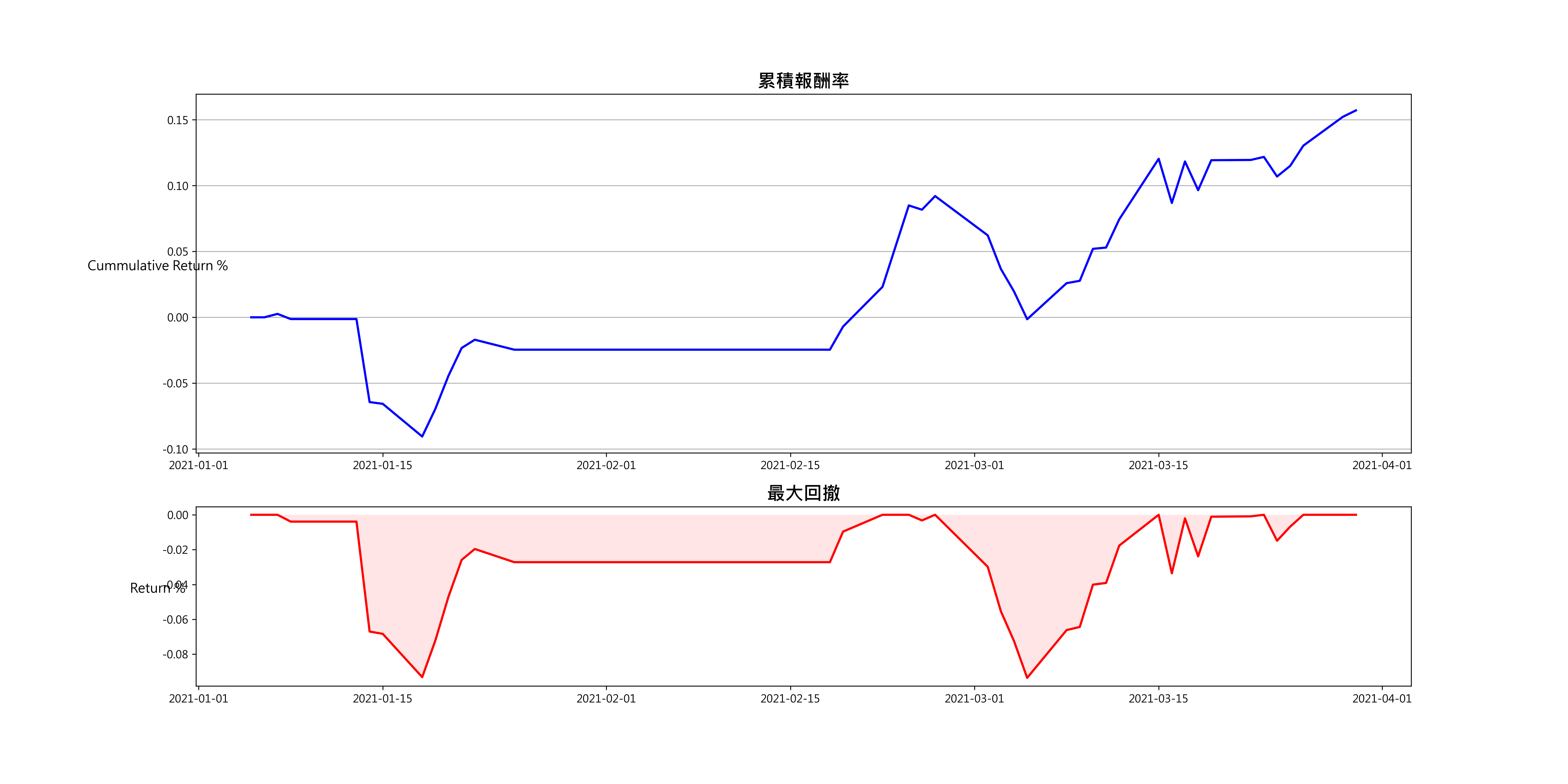
由最大回档图可以发现有两次的配对交易最大回档都连续跌破8%，代表策略的停损机制做的不是太好，或是 μ均值与 σ标准差参数失灵。未来可以试著调降2.5σ的标准，或是以rolling的方式计算形成期价差序列的 μ均值与 σ标准差，因为海运股在2021年上半年的波动性极大，而交易期刚好落在2021年1月至3月，形成期则是2020年1月至12月。

本文仅供参考之用，并不构成要约、招揽或邀请、诱使、任何不论种类或形式之申述或订立任何建议及推荐，读者务请运用个人独立思考能力，自行作出投资决定，如因相关建议招致损失，概与作者无涉。

完整程式码

点此前往Github