Photo by Isaac Smith on Unsplash
目录
首先,本文会执行模型建置的过程,让读者了解Python套件的应用,但是不会进行上篇文章中提及的任何检定,以避免篇幅冗长;接著,计算预测报酬以及价格;最后将以视觉化方式比对真实历史价格,来检讨ARMA-GARCH模型的预测效果。
Note:本文是利用”ARMA”模型对报酬率建模,而非上篇文章中的”ARIMA”,其差异处仅在ARIMA能够处理非定态数据。上篇使用ARIMA是想尽量让读者了解时间序列的原理,而本文使用ARMA是想让读者多了解一种方法。
本文使用 MacOS 并以 Jupyter Notebook作为编辑器
import numpy as npimport pandas as pdimport matplotlib.pyplot as plt%matplotlib inlineimport seaborn as snssns.set()import tejapitejapi.ApiConfig.api_key = 'Your Key'tejapi.ApiConfig.ignoretz = True
Step 1. 资料捞取
data = tejapi.get('TWN/APRCD', # 公司交易资料-收盘价coid= '0050', # 台湾50mdate={'gte': '2003-01-01', 'lte':'2021-12-31'},opts={'columns': ['mdate', 'close_d', 'roi']},chinese_column_name=True,paginate=True)data['年月日'] = pd.to_datetime(data['年月日'])data = data.set_index('年月日')data = data.rename(columns = {'收盘价(元)':'收盘价', '报酬率%':'日报酬率(%)'})
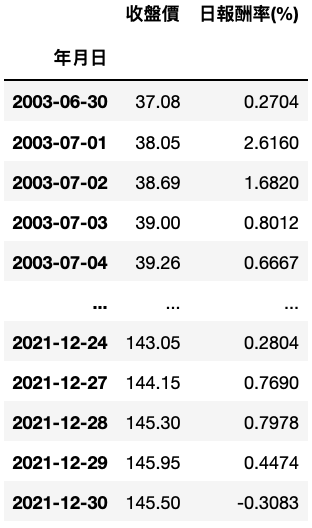
Step 2. 资料分割
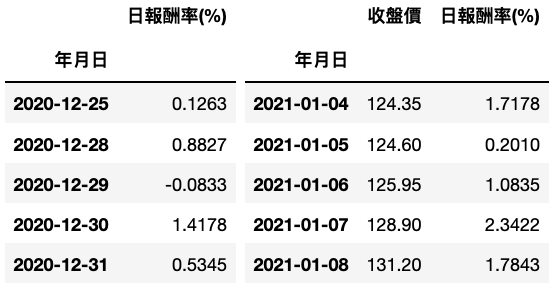
train_date = data.index.get_level_values('年月日') <= '2020-12-31'train_data = data[train_date].drop(columns = ['收盘价'])test_data = data[~train_date]# 保留test_data收盘价,用来比对模型预测值
Step 3. ARMA参数选择
本文会利用statsmodels进行参数筛选,与上篇利用pmdarima不同。
import statsmodels.api as sm# AIC、BIC准则sm.tsa.stattools.arma_order_select_ic(train_data, ic=["aic", "bic"])
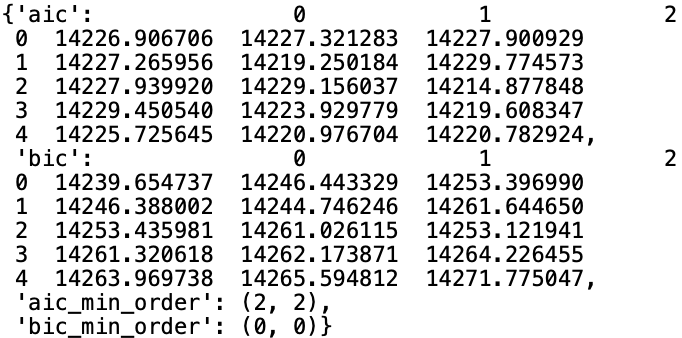
可以看到BIC准则的参数挑选项目为(0,0),这是源于BIC准则会对多解释变数进行较严格的筛选,因此,本文选择(p,q)=(2,2),进行模型建置。
Step 4. ARMA模型建置
from statsmodels.tsa.arima_model import ARMAmodel = ARMA(train_data, order = (2, 2))arma = model.fit()print(arma.summary())
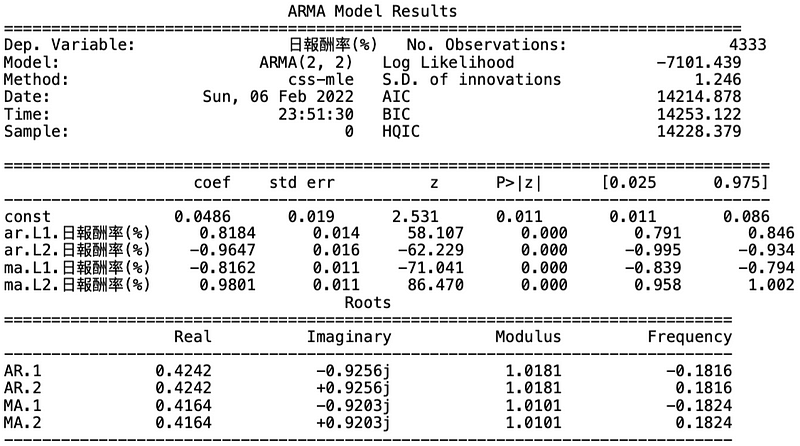
Step 5. GARCH模型建置
# 取得ARMA模型的残差项目arma_resid = list(arma.resid)from arch import arch_modelmdl_garch = arch_model(arma_resid, vol = 'GARCH', p = 1, q = 1)garch = mdl_garch.fit()print(garch.summary())
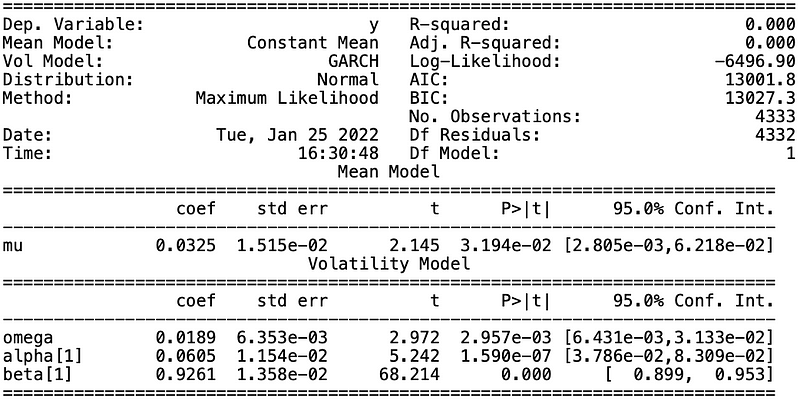
在预测的部分,本文会用ARMA模型估计平均,并应用GARCH模型预测波动区间。
Step 1. ARMA预测平均报酬
# len(train_data) = 4333, len(data) = 4577 forecast_mu = arma.predict(start = 4333, end = 4576) # 预测函式的end包含当期,所以需进行4577-1=4576。
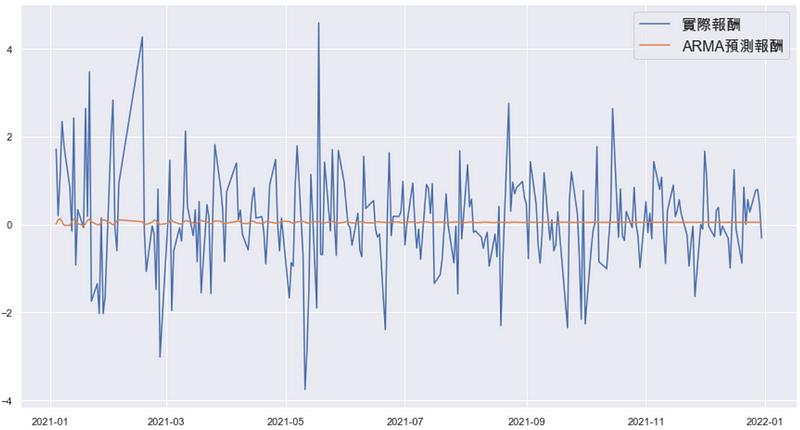
从上图发现经过一段时间后,预测平均报酬会逐渐成为趋近于0的常数,仅在预测初期有较明显的波动。
Step 2. GARCH预测波动度
garch_forecast = []for i in range(len(test_data)):train = arma_resid[:-(len(test_data)-i)]model = arch_model(train, vol = 'GARCH', p = 1, q = 1)garch_fit = model.fit()prediction = garch_fit.forecast(horizon=1)garch_forecast.append(np.sqrt(prediction.variance.values[-1:][0]))
本文此处运用滚动式的方法预测各期的波动度,所以上述程式码是将GARCH模型包在回圈当中,再回传储存值。接下来,先将上述各预测值存入test_data,并计算上下区间,供后续计算。
test_data['ARMA预测报酬(%)'] = list(forecast_mu)test_data['GARCH预测波动度'] = (garch_forecast)test_data['预测区间上限'] = test_data['ARMA预测报酬(%)'] + test_data['GARCH预测波动度']test_data['预测区间下限'] = test_data['ARMA预测报酬(%)'] - test_data['GARCH预测波动度']
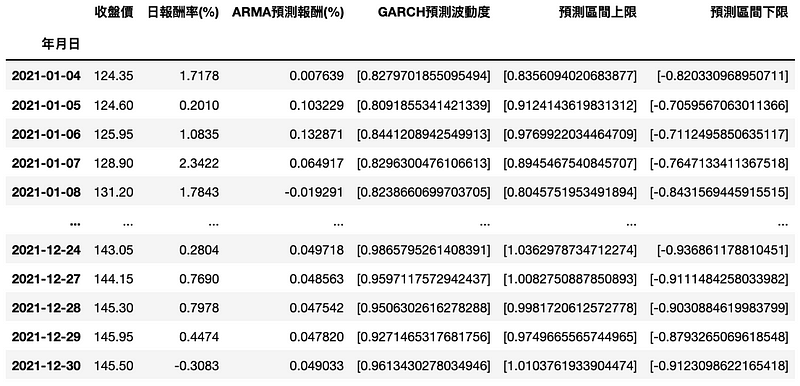
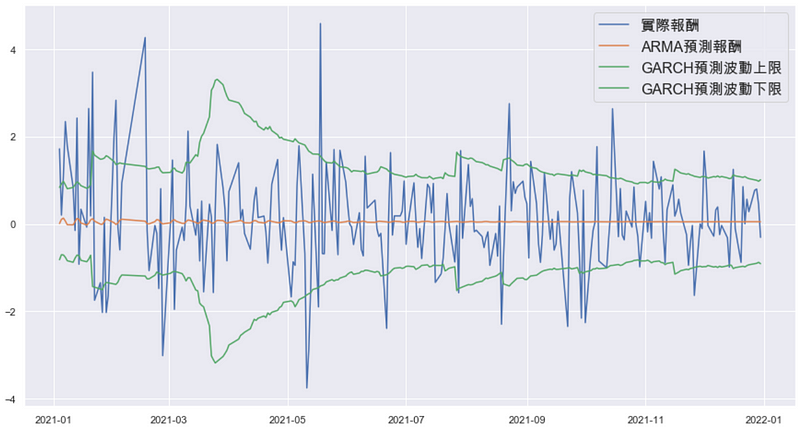
根据上图,大部分的实际报酬率是包含在区间当中的;然而,无法有效预测单一日期波动幅度较大之报酬率。
Step 3. 预测价格
# 本文已经把train_data中的价格删除,所以需重新计算2020-12-30的收盘价first_price = test_data['收盘价'][0] / (1+test_data['日报酬率(%)'][0]*0.01)# 计算第一期预测test_data['ARMA预测价格'] = first_price * (1 + test_data['ARMA预测报酬(%)']*0.01)test_data['预测价格区间上限'] = first_price * (1 + test_data['预测区间上限']*0.01)test_data['预测价格区间下限'] = first_price * (1 + test_data['预测区间下限']*0.01)# 计算剩余预测区间for i in range(1, len(test_data)):test_data['ARMA预测价格'][i] = test_data['预测价格'][i-1] * (1 + test_data['ARMA预测报酬(%)'][i]*0.01)test_data['预测价格区间上限'][i] = test_data['预测价格区间上限'][i-1] * (1 + test_data['预测区间上限'][i]*0.01)test_data['预测价格区间下限'][i] = test_data['预测价格区间下限'][i-1] * (1 + test_data['预测区间下限'][i]*0.01)# 计算区间均价test_data['预测平均价格'] = (test_data['预测价格区间上限'] + test_data['预测价格区间下限']) / 2
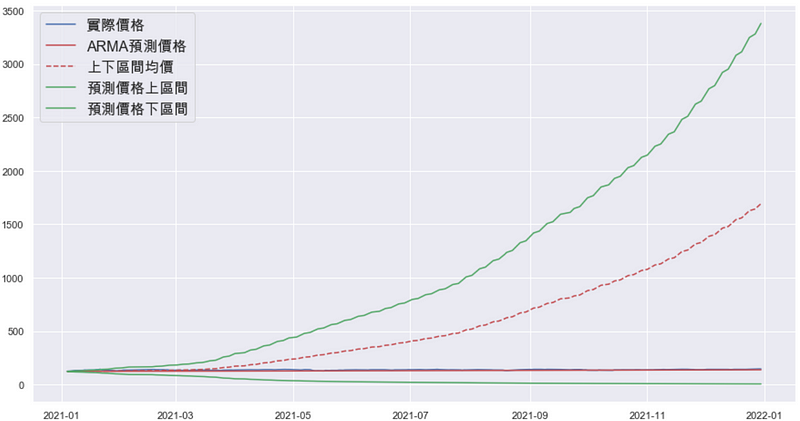
上图显示,在预测初期时,预测区间较窄,并且两项价格预测值也与实际价格相去不远;然而,随著预测时间越往后,预测区间扩大、区间均价偏移,导致无法准确判断模型的成效。所以本文接下来会展示时间轴为两个月的预测值。
new_date = test_data.index.get_level_values('年月日') <= '2021-03-01'new_test = test_data[new_date]
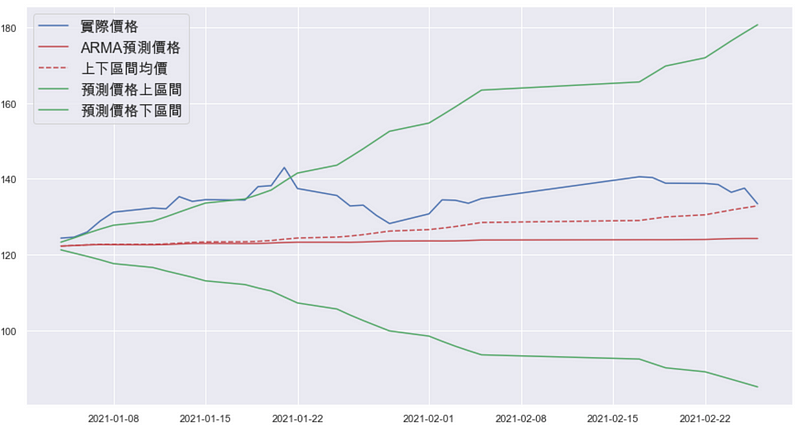
在两个月的区间中,读者应该可以更清楚地发现,实际价格与预测值间的差异。首先,是两项预测价格与实际价格的关系,可以发现区间均价更贴近实际价格;而在区间预测方面,随著预测区间扩大以及实际价格回落,实际价格的走势才涵盖在预测波动当中。
借由最后的结果,读者应该可以明白此次ARMA-GARCH模型对0050并没有很好的预测效果,尽管在模型配适上有不错的成果。先不论随时间推移而区间扩大,导致失去判断标准这项问题,毕竟时间轴越远,本来就应该进行更保守的估计;单就预测初期的结果,便可以发现实际价格超出模型预测的波动区间,也就代表模型在初期预测便没有足够的可信度,这可能是源于本文并无考量到的外生变量或是季节性因素而造成的。所以,若是读者对这类型的议题有兴趣,请持续关注此平台的文章;另外,欢迎选购 TEJ E Shop中的方案,就能够轻松地对有兴趣的标的,实作走势预测。

电子报订阅