Lasso 回归模型

Mar 29 2022

Lasso模型 — Photo by Luke Chesser on Unsplash

本文重点概要

文章难度：★★☆☆☆
以Lasso模型寻找有效经济成长率的变数因子
阅读建议：本文首先会进行总经资料的挑选以及前处理，再执行模型拟合，内文的叙述并不会讨论数学模型，仅会文字讲述内涵，以增进易读性，但需要读者对回归模型有基本认识，至于Lasso模型的概念，会在以下「前文」当中说明。

前言

Lasso模型的全称为最小绝对值收敛和选择算式，主要运用在回归分析中的解释变数筛选并通过「惩罚项目」的参数设定调整复杂度，因此，透过Lasso模型便可以降低「过度拟合」的问题，并且提升解释变数的有效性。

Lasso模型的惩罚项用于衡量「误差项」与「解释变数量」之间孰轻孰重，也就是在挑选模型参数的过程中便不会只参考误差项最小化，还会综合考量解释变数的数量不要太多，让模型有适当的复杂度。

惩罚项参数设定则会影响到模型会考虑哪一个面相较多，若参数小，则该模型较注重「减少误差」；反之，参数大，则模型较注重「减少解释变数的量」，所以这就需要执行人员选定一个区间的数值不断进行测试。

Note:惩罚项参数的设定需大于 0，才会符合想要考虑越少参数越好的这项条件；此外，Python套件中惩罚项参数设定为Alpha栏位。

编辑环境及模组需求

本文使用 MacOS 并以 Jupyter Notebook作为编辑器

# 基本功能
import numpy as np
import pandas as pd

# 绘图
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
sns.set()

# TEJ API
import tejapi
tejapi.ApiConfig.api_key = 'Your Key'
tejapi.ApiConfig.ignoretz = True

资料库使用

总体经济说明表：针对总体经济表的科目所使用的说明表，资料代码为(GLOBAL/ABMAR)。

总体经济表：政府部门发布的总体经济指标，来源包含IMF与OECD，以及相关专业刊物。资料代码为(GLOBAL/ANMAR)。

资料挑选

Step 1. 读取资料基本讯息

factor = tejapi.get('GLOBAL/ABMAR',
                opts={'columns': ['coid','mdate', 'cname', 'freq']},
                chinese_column_name=True,
                paginate=True)

Step 2. 挑选特定资料

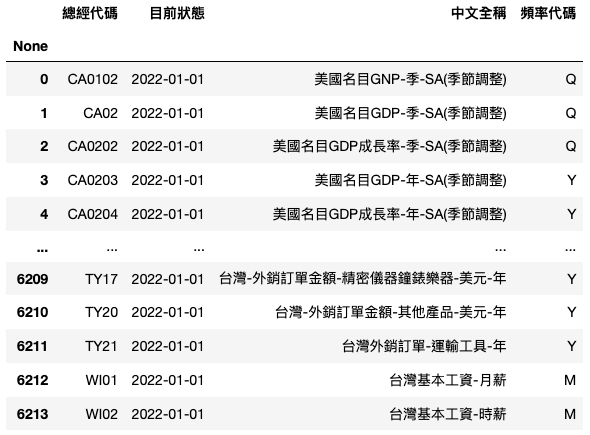
# 挑选资料
list1 = list(factor['总经代码'][i] for i in range(0,6214) if '台湾' in factor.iloc[i,2] and factor['频率代码'][i] == 'Q')

# 整理表格
factor = factor[factor['总经代码'].isin(list1)].reset_index().drop(columns =['None', '目前状态', '频率代码'])

因为总经指标种类繁多，不可能将所有的数据都考虑进模型当中，所以本文仅会考虑「台湾的资料」；此外，因为经济成长率的统计周期为每季，因此也仅会考量「季资料」。

Step 3. 读取指标数据

data = tejapi.get('GLOBAL/ANMAR',
                  mdate={'gte': '2008-01-01', 'lte':'2021-12-31'},
                  opts={'columns': ['coid','mdate', 'val', 'pfr']},
                  coid = list1, # 符合条件的指标
                  chinese_column_name=True,
                  paginate=True)

数据前处理

Step 1. 移除预测值资料

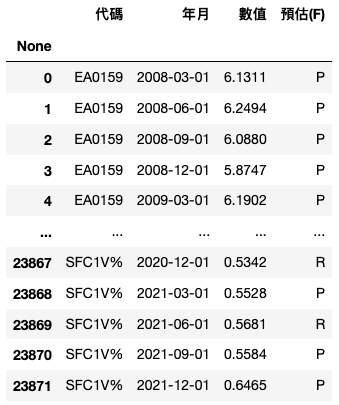
data = data[data['预估(F)'] != 'F']

本文在数据方面的考量会将预估值排除。

Step 2. 表格整理

data = data.set_index('年月')

df = {}

for i in list1:
    p = data[data['代码'] == i]
    p = p['数值']
    df.setdefault(i, p)

df = pd.concat(df, axis = 1)

先设定「年月」为index，再透过回圈列出各别指标的数据，最后将其并列排序。

Step 3. 选择经济成长率指标

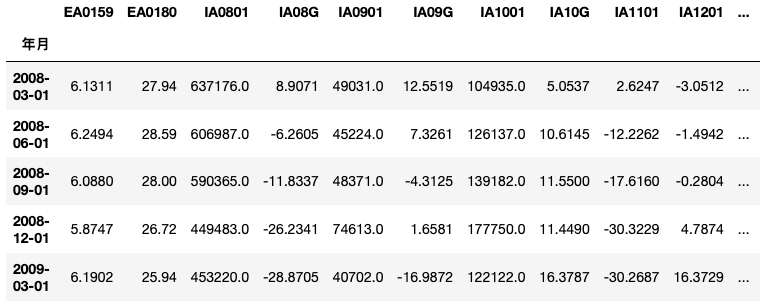
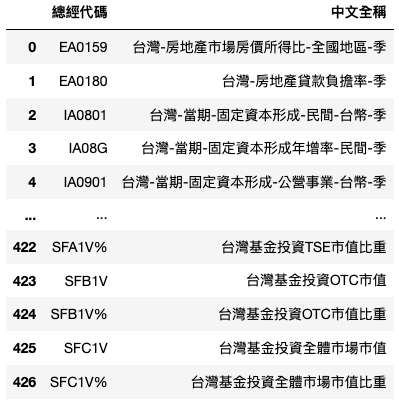
# 列出所有经济成长率指标
growth_reference = list(factor['总经代码'][i] for i in range(0,427) if '经济成长率' in factor.iloc[i,1])

factor[factor['总经代码'].isin(growth_reference)]

# 选定'NE0904-季节调整后年化经济成长率'作为经济成长率指标
growth = df['NE0904']

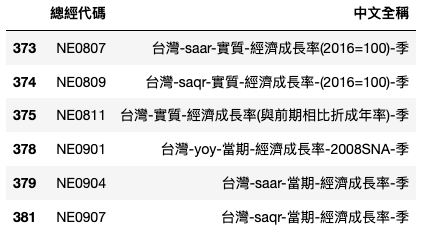
季节调整后年化经济成长率'作为经济成长率指标 — 季节调整后年化经济成长率’作为经济成长率指标

本文考量到台湾是出口贸易导向的国家，经济容易受到全球消费循环影响，所以选择「NE0904-季节调整后年化经济成长率(saar)」为本文的经济成长率依据。

# 移除各项经济成长率指标
df = df.drop(columns = growth_reference)

# 移除具有缺失值的指标
df = df.dropna(axis = 1, how = 'any')

Step 4. 定态检定

from statsmodels.tsa.stattools import adfuller
    
for i in df.columns.values:
    p_value = adfuller(df[i])[1]
    if p_value > 0.05:
        df = df.drop(columns = i)
        
df = df.dropna(axis = 1, how = 'any')

print('解释变数量：', len(df.columns))
print('经济成长率定态检定Ｐ值：', '{:.5f}'.format(adfuller(growth)[1]))

透过回圈对各解释变数进行定检定，并且设定若为非定态的数据便直接踢除，不再进行差分或变动率的计算；另外，在末端也统计解释变数的总量，总共有148个；最后，进行经济成长率的检定，检定结果P值为0.0000，因此符合定态的条件。

模型拟合

Step 1. 套件导入＆资料分割

from sklearn.linear_model import Lasso
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures

df_train = df.head(45)
df_valid = df.tail(10)

growth_train = growth.head(45)
growth_valid = growth.tail(10)

Step 2. 模型拟合

内文仅呈现大惩罚项(Alpha)的模型程式码，中、小Alpha的内容与其皆相同，而考量到篇幅，此处不呈现该过程。(详见完整程式码)

# 大alpha模型

Lasso_l = Pipeline(steps = [('poly', PolynomialFeatures(degree = 1)), ('Lasso', Lasso(alpha = 1000))])
large = Lasso_l.fit(df_train, growth_train)
growth_pred_l = large.predict(df_valid)
large_alpha = list(growth_pred_l)

print('大Alpha的MSE:', metrics.mean_squared_error(growth_valid, large_alpha))

考量到解释变数量总共有148个，本次模型变仅考虑各变数本身的影响力，并不考虑交互作用，所以degree的部分设定为1；此外，在设定惩罚项时，以Alpha=10, 100, 1000为三个级距，尽量让模型在挑选变数上更为严格。

最后列印出各模型的MSE，如下：

大Alpha的MSE: 207.82

中Alpha的MSE: 526.29

小Alpha的MSE: 1399.59

由上列比较可以认知到，惩罚项目较大的模型表现较好，以下将透过图表查看，并选择最终运用的模型。

模型比较＆寻找有效变数

Step 1. 表格整理

pred_data = {'小Alpha预测值': small_alpha, '中Alpha预测值': medium_alpha, '大Alpha预测值':large_alpha}
result = pd.DataFrame(pred_data, index = growth_valid.index)
final = pd.concat([growth_valid, result], axis = 1)
final = final.rename(columns={'NE0904':'实际经济成长率'})

Step 2. 表格视觉化

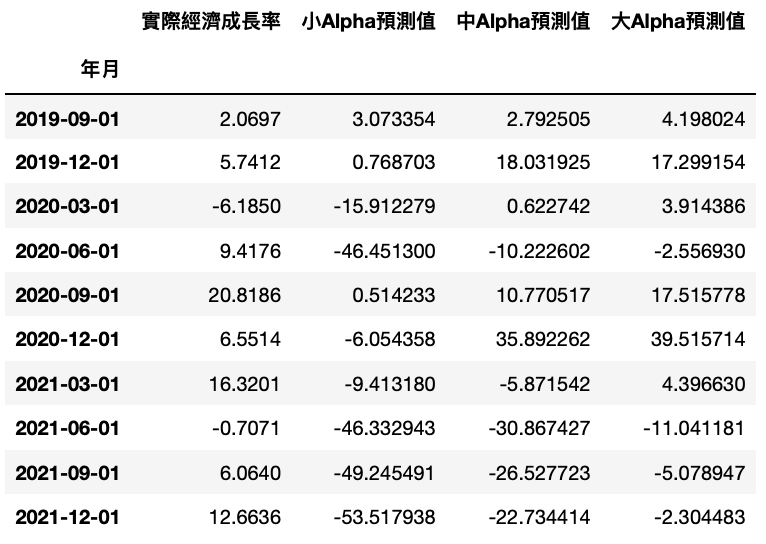
# 让python套件运用中文文字
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS']

plt.figure(figsize=(15,8))

plt.plot(final['实际经济成长率'])
plt.plot(final['小Alpha预测值'])
plt.plot(final['中Alpha预测值'])
plt.plot(final['大Alpha预测值'])

plt.legend(('实际成长率', '小Alpha预测', '中Alpha预测', '大Alpha预测'), fontsize=16)

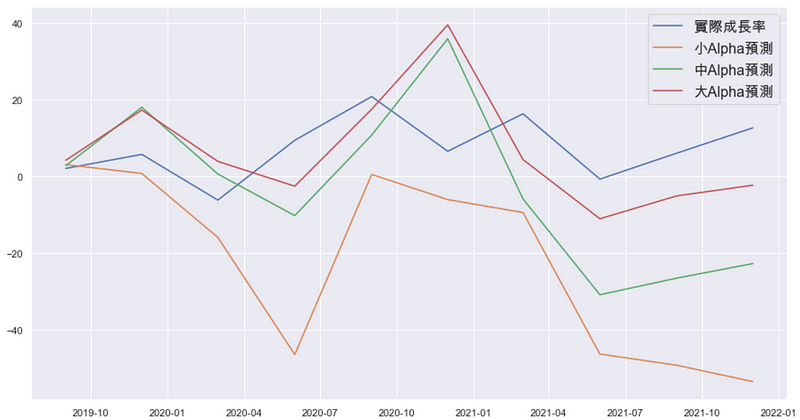
透过图表可以清楚比较，大、中、小三个惩罚项参数级距的模型，的确是大Alpha的模型预测结果最贴近实际情形，因此本文后续便以该模型寻找有效经济成长解释变数。

Step 3. 有效变数

# 重新拟合一次模型
lasso = Lasso(alpha = 1000)
mdl = lasso.fit(df_train,growth_train)

# 列出系数大于0的变数
lasso_coefs = pd.Series(dict(zip(list(df_valid), mdl.coef_)))
coefs = pd.DataFrame(dict(Coefficient=lasso_coefs))
coid = coefs[coefs['Coefficient'] > 0].index

# 回传变数代号寻找中文名称
factor[factor['总经代码'].isin(coid)]

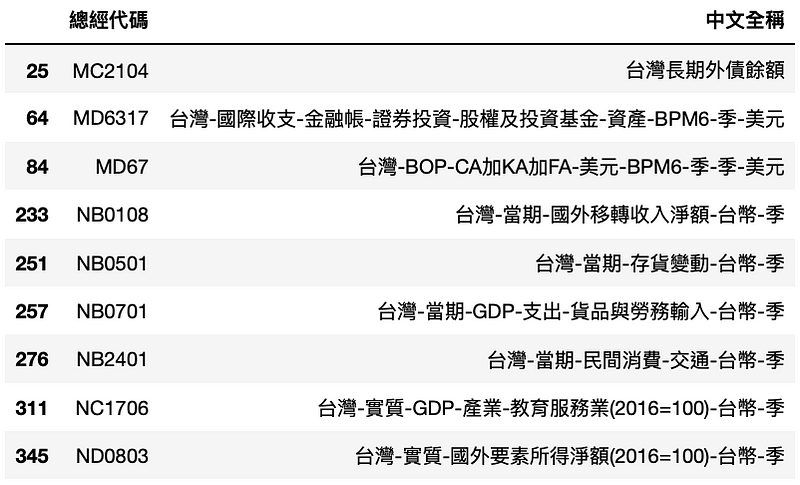
从上表可以看出，主要的有效变数由贸易、国际金融等相关数据组成，符合台湾作为出口贸易导向国家的情形；此外，从教育服务业的GDP这个项目，也可以了解人口教育素质的提升，对经济成长亦有所驱动，因此培育下代人才也是台湾需要持续关注的议题。

结论

借由上述的过程，本文首先示范资料的筛选以及前处理；接著进行模型的拟合与比较；最终找出影响经济成长的有效变数。当然，在资料处理的阶段，本文为求篇幅尽量简短，没有进行更多的资料转换或差分等程序，这是读者可以自行选择处理的，并不一定要依照本文的处理方式；此外，在模型的参数设定中，我们也鼓励读者后续用不同的组合试做，实际体验一遍这样的过程，相信会更有收获。最后，若读者对于模型建置有兴趣，又苦于没有齐全的资料，欢迎选购 TEJ E Shop中的方案，相信读者具有完整的资料库后，就能轻易完成自己的模型建置。

完整程式码

点此前往Github