SVM 模型

Apr 20 2022

本文重点概要

文章难度：★★★☆☆
财务数据拟合SVM模型并进行分数检验
阅读建议：本文首先进行变数筛选以及资料前处理；接著执行模型适配；最后检视模型胜率分数并视觉化其结果。以下前文会说明SVM模型的运作架构，虽不会论及数学公式，但需要读者对统计分析(例如：过度拟合、线性等)有基本的概念。

前言

Support Vector Machine(简称SVM)模型中文全称为支援向量机，是一种基于统计原理的机器学习演算法，应运用于资料分类(Classifier)以及回归(Regressor)，本文会以资料分类为主进行。

SVM进行分类的过程，简单来说便是以直线或不规则的线切分不同属性的资料。至于要如何画出最佳解的线，需要考虑两个问题，首先便是资料属性的差异程度，简单来说即如果一条线越宽，则代表他能够辨识资料差异的程度越好；其次则是分类误差，因为在实务操作上不太可能全然地将不同属性的资料分割，所以也要考量到误差的大小，运作方式为设定误差惩罚项系数。而上述两项标准孰轻孰重，则需要模型操作人员设定参数，文中会再说明。

编辑环境及模组需求

本文使用 MacOS 并以 Jupyter Notebook作为编辑器

# 基本功能
import numpy as np
import pandas as pd

# 绘图
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
sns.set()

# TEJ API
import tejapi
tejapi.ApiConfig.api_key = 'Your Key'
tejapi.ApiConfig.ignoretz = True

资料库使用

证券属性资料表：台湾全市场证券标的属性资料，资料代码为(TWN/ANPRCSTD)。

财务资料表(季)：提供基础财务资料，单季资料，非累积资料。资料代码为(TWN/EWIFINQ)。

上市(柜)未调整股价(日)：上市证券及指数(TSE及OTC)的交易面资料。资料代码为(TWN/APRCD)。

资料处理

Step 1. 处理证券属性资料

sec_code = tejapi.get('TWN/ANPRCSTD', chinese_column_name = True)

condition = (sec_code['上市别'] == 'TSE') & (sec_code['证券种类名称'] == '普通股')

pub_common_stk = sec_code.loc[condition, '证券码'].to_list()

筛选证券标的为台湾股票市场并且设定范围仅考虑普通股。

Step 2. 导入财务资料

fin_data = tejapi.get('TWN/EWIFINQ',
          coid = pub_common_stk, 
          mdate= {'gte': '2017-01-01', 'lte': '2021-12-31'},
          opts={'columns': ['coid', 'mdate', 'ac_r103', 'ac_r403']},
          paginate = True,
          chinese_column_name = True)
fin_data = fin_data.dropna()

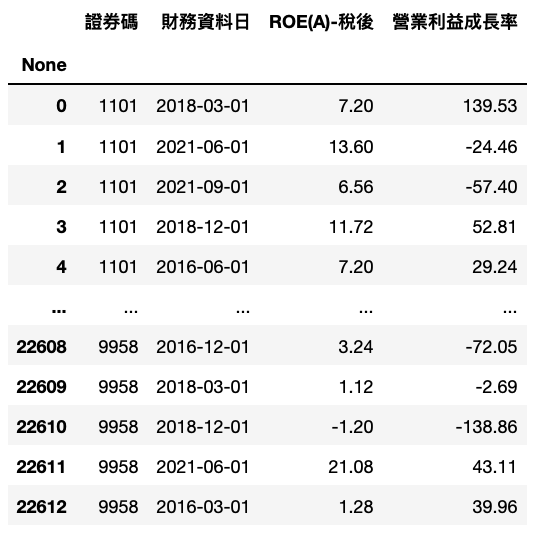
本文这次将应用的财务资料为税后ROE以及营业利益成长率，并假设要这两项指标皆越大越好，其意涵如下：

税后ROE：中文全称为股东权益报酬率，也就是公司利用股东自有资本营利的能力。

营业利益成长率：首先营业利益率是公司营业利益占营业收入的比率，也就是衡量公司本业营业效率的指标，而其成长率则是检验公司是否具有稳定成长的现象。

本文选择这两项指标是希望能够在短中期的投资区间取得一个平衡，会这样假设是因为考量到ROE虽然是衡量公司盈利能力的有力指标，但通常会受到产业淡旺季、公司资本结构变化的影响，所以将营业利益成长率作为公司营业本质的标准，减少ROE单一指标的不足。

Step 3. 导入股价资料＆资料合并

price_df = pd.DataFrame()
for i in pub_common_stk:
    price_data = tejapi.get('TWN/APRCD',
               coid = i, 
               mdate= {'gte': '2016-01-01', 'lte': '2021-12-31'},
               opts={'columns': ['coid', 'mdate', 'close_d']},
               paginate = True,
               chinese_column_name = True
               )
    price_df = pd.concat([price_df, price_data], axis = 0)

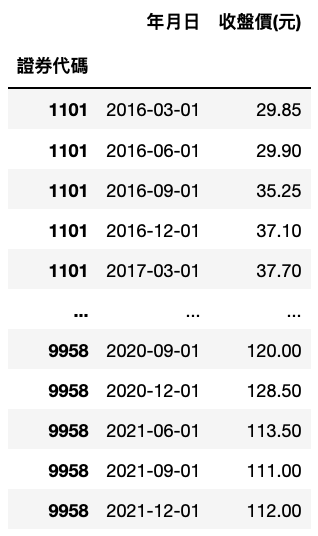
导入符合标的之每日收盘价格。

def compare(df1, df2):
    df2 = df2.rename(columns = {'证券码':'证券代码', '财务资料日':'年月日'})
    compare = pd.merge(df1, df2, how='inner', on=['证券代码', '年月日'])
    result1 = pd.concat([compare['年月日'], compare['证券代码']], axis = 1)
    result2 = pd.merge(df1, result1, how='inner', on =['证券代码', '年月日'])
    return result2

ret_df2 = compare(price_df, fin_data)
ret_df2 = ret_df2.set_index(['证券代码'])

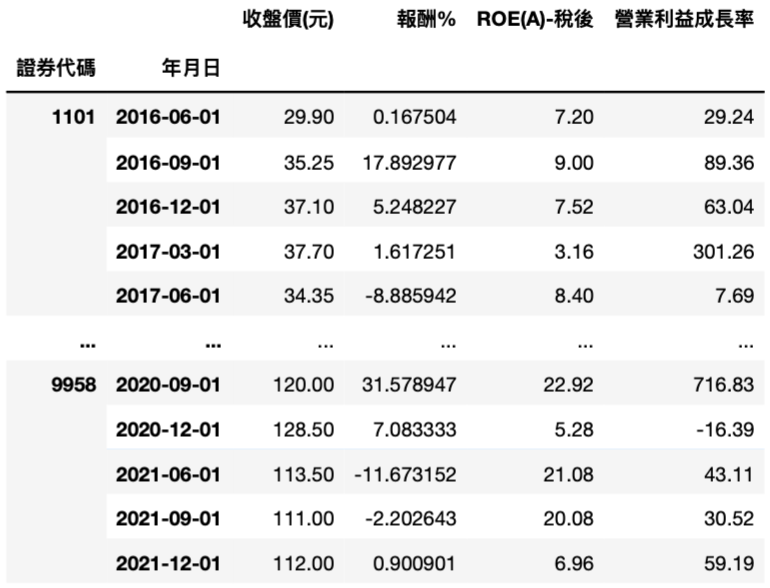
合并财务资料表与股价资料，并只留下财务资料日期(转换名称为年月日)与价格资料，后续将计算每次财务资料揭示间的买入持有报酬。

Step 4. 计算报酬资料＆资料最后整理

ret_df2['报酬%'] = pd.Series()
for i in ret_df2.index.values:
    ret_df2.loc[i]['报酬%'] = pd.Series(ret_df2.loc[i]['收盘价(元)']).pct_change(1)*100
ret_df2 = ret_df2.dropna().reset_index()

这边要注意，需要透过回圈导入不同标的资料，分别计算报酬。不能直接对资料表取变动值，因为不同标的是直接叠在一起的，若是直接取变动值，则从第二项标的开始之首个报酬会跟前一项标的资料混在一起计算。

def compare2(df1, df2):
    df2 = df2.rename(columns = {'证券码':'证券代码', '财务资料日':'年月日'})
    compare = pd.merge(df1, df2, how='inner', on=['证券代码', '年月日'])
    return compare

data = compare2(ret_df2, fin_data).set_index(['证券代码','年月日'])

Step 5. 离群值处理

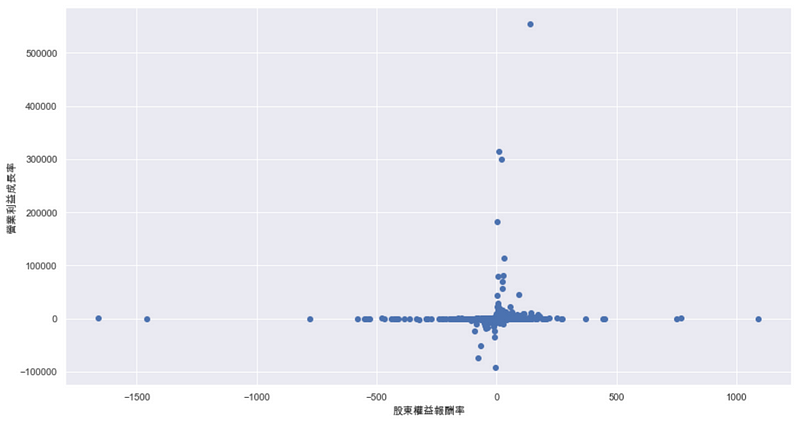
透过上图可以发现，不论在ROE或是营业利益率两方面的资料，皆有很严重的离群值现象，因此本文后续将以超出标准差为依据，将离群值从样本中移除。(因应篇幅考量，此处理过程请详见完整程式码)

Step 6. 资料分配标准化

import sklearn.preprocessing as preprocessing

data_rmout = data_no.replace([np.inf, -np.inf], np.nan)
data_rmout = data_no.dropna()
data_std = pd.DataFrame(preprocessing.scale(data_no), index = data_no.index, columns = data_no.columns)

plt.figure(figsize=(15,8))
plt.hist(data_std['ROE(A)-税后'], bins = 50)
plt.hist(data_std['营业利益成长率'], bins = 50, alpha =0.7)

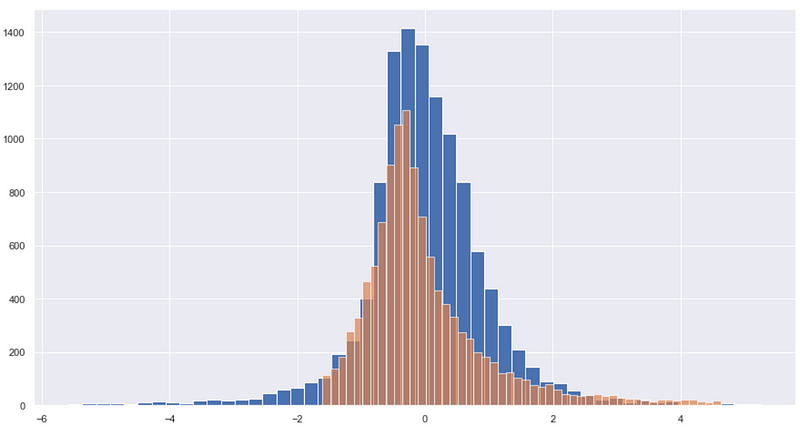
透过上图可以清楚观察到，两项数据的分配已经通过标准化的程序，分布情形相似。

模型建置

Step 1. 资料分割

from sklearn.model_selection import train_test_split

data_train, data_test = train_test_split(data_std, test_size = 0.2, random_state = 0)

Step 2. 模型拟合

from sklearn.svm import SVC

cf = SVC(
C=10.0, break_ties=False, cache_size=200, class_weight=None, coef0=0.0,decision_function_shape='ovr', degree=3, gamma='scale', kernel='linear',max_iter=-1, probability=False, random_state=None, shrinking=True,tol=0.001, verbose=False
)

index = ['ROE(A)-税后', '营业利益成长率']

cf.fit(data_train[index], data_train['报酬%'] >  data_train['报酬%'].quantile(0.5))

在上方程式码中可以看到本文使用的方法是线性结构，而也考量到线性结构可能会使模型太过简单，所以设定分类错误的惩罚项系数为10，提高模型的复杂度；在模型拟合的指令中，本文则是设定标准为各样本报酬率要大于中位数。

Step 3. 资料分类视觉化

from mlxtend.plotting import plot_decision_regions

index_plot = data_test[index].values
labels_plot = (data_test['报酬%'] > data_test['报酬%'].quantile(0.5)).astype(int).values

plot_decision_regions(index_plot, labels_plot, cf)
plt.xlabel('股东权益报酬率')
plt.ylabel('营业利益成长率')

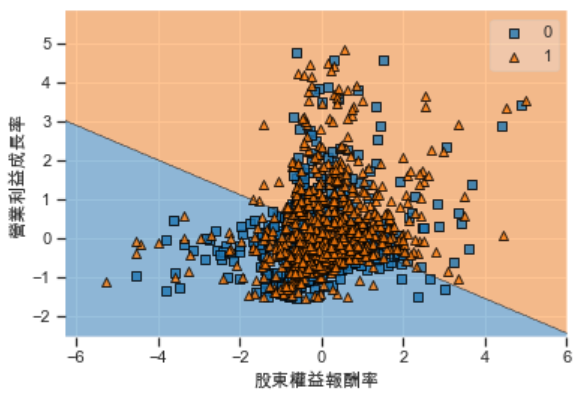
从图中可以知道模型判断ROE越高且营业利益成长率越高的样本是具有增长潜力的，这与我们先前的假设相同。

Step 4. 检验结果

# TRAIN
cf.score(data_train[index], data_train['报酬%'] >  data_train['报酬%'].quantile(0.5))

# TEST
cf.score(data_test[index], data_test['报酬%'] >  data_test['报酬%'].quantile(0.5))

训练资料集分数：0.5857

验证资料集分数：0.5965

从上述结果了解两项资料集的分数皆大于0.5，代表模型的有效性有一定基础，并且验证资料集分数略高训练资料集也让说明应该没有过度拟合的情形。

结论

上述的内文首先示范资料筛选以及前处理；接著进行模型的拟合、视觉化与检验。在资料处理阶段，本文说明所选择的财务资料及其背后意涵，若读者有更偏好的资料，欢迎至TEJ资料库中搜集；随后，在模型阶段，本文挑选较简单的线性结构，让读者了解基本的模型参数设定，并且通过视觉化模型所分析的结果，验证「两项指标皆越大越好的假设」，最后再计算训练集与验证集的分数，确定模型的效力。

本文至此为止，欢迎对于机器学习模型有兴趣的读者，持续关注本平台，后续会有更多文章说明其他应用；此外，也欢迎读者选购 TEJ E Shop中的方案，相信读者具有完整的资料库后，读者就能轻易练习建立自己模型。

完整程式码

点此前往Github