
目录
风险值的意思基本上就是根据给定的信赖水准以及某特定期间,投资组合可能产生的最大损失。本文计算过程如下:
在计算风险值的方面,需要注意各项参数的使用,以及资产报酬率的分布情形,才能够将真实的市场波动反映在计算数值上,后续本文将详细说明完整的执行过程,以及本文所用的「变异数-共变异数法」在应用上的优缺点。
本文所用之风险值名词如下:
1.每日盈余风险(Daily Earning at Risk, DEAR):投资标的之单日风险值。
2.相对风险值(Relative VaR):投资标的相对于投资报酬率均值的风险值。
(|-α| * σ) * portfolio value
3.绝对风险值(Absolute VaR):投资标的相对于0的风险值。
(|-α| * σ – mean) * portfolio value
上述α皆为常态分配的临界值,下文计算会使用99%信心水准的z值,2.33。
本文使用 MacOS 并以 Jupyter Notebook 作为编辑器
#基本套件import numpy as npimport pandas as pd#绘图套件import matplotlib.pyplot as plt%matplotlib inlineimport seaborn as snssns.set()#TEJAPIimport tejapitejapi.ApiConfig.api_key = 'Your Key'tejapi.ApiConfig.ignoretz = True
本文投资组合以传产、电子、金融及航运各一支标的组成;内文会搭配讲解风险值计算的方法和各类型标的报酬率分布情形,让读者更加了解风险值计算上的优缺点。
ticker = ['1476', '2330', '2882', '2603']# 儒鸿, 台积电, 国泰金, 长荣df = tejapi.get('TWN/EWPRCD', # 公司交易资料-已调整股价(收盘价)coid = ticker,mdate = {'gte':'20200101', 'lte':'20220225'},opts = {'columns': ['coid', 'mdate', 'close_adj']},chinese_column_name = True,paginate = True)df = df.set_index('日期')
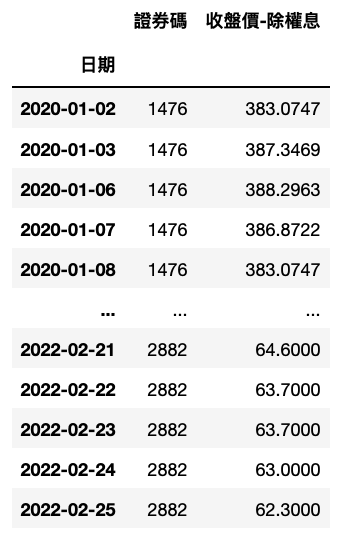
data = {}for i in ticker:p = df[df['证券代码'] == i]p = p['收盘价(元)']data.setdefault(i, p)data = pd.concat(data, axis = 1)
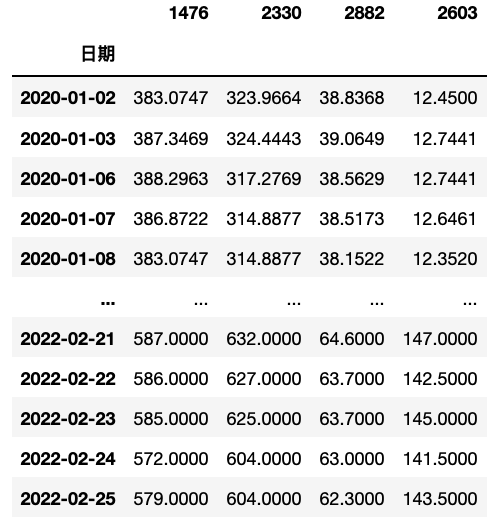
本文此处取用报酬率资讯表,确保资料来源的正确性,而资料处理过程与上述价格资料相同。
ret = tejapi.get('TWN/EWPRCD2',coid = ticker,mdate = {'gte':'20200101', 'lte':'20220225'},opts = {'columns': ['coid', 'mdate', 'roia']},chinese_column_name = True,paginate = True)ret = ret.set_index('日期')data2 = {}for i in ticker:r = ret[ret['证券码'] == i]r = r['日报酬率(%)']data2.setdefault(i, r)data2 = pd.concat(data2, axis = 1)data2 = data2 * 0.01 #还原报酬率为百分之一单位基准
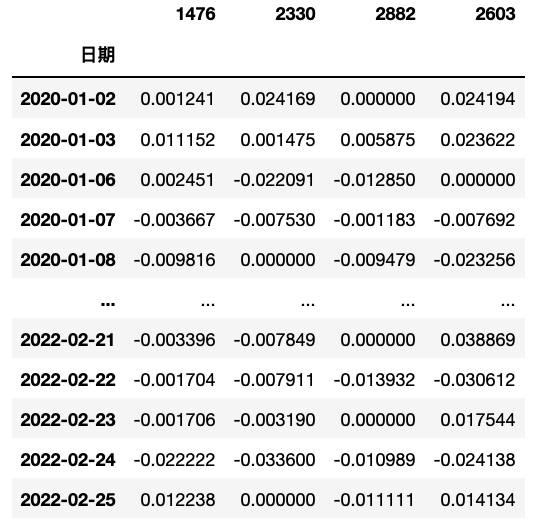
value = data.iloc[-1] * 1000Mean = []STD = []MAX = []Min = []abs_var = []re_var = []
首先,根据股价资料最后一日计算各项标的价值,本文是以至少持有一张股票为单位;接著,定义各项空list。
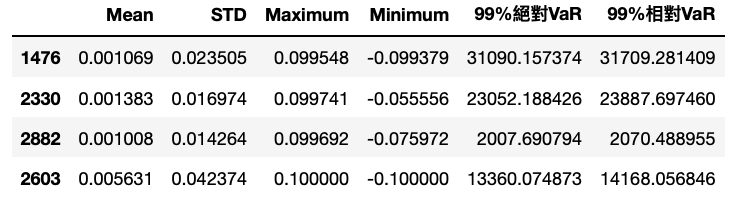
for i in ticker:v = data2[i].std() # Standard Errormean = data2[i].mean() # Meanmaximum = data2[i].max() # Maximumminimum = data2[i].min() # Minimum# Calculate 99% Absolute VaRvar_99_ab = (abs(-2.33)*v - mean) * value[i]# Calculate 99% Relative VaRvar_99_re = (abs(-2.33)*v) * value[i]# Append those values in listsMean.append(mean)STD.append(v)MAX.append(maximum)Min.append(minimum)abs_var.append(var_99_ab)re_var.append(var_99_re)
在回圈中,先计算各项标的之标准差、平均数及最大最小值;再计算绝对风险值与相对风险值;最后将上述计算各数值回传至相对应的list。
在风险值的计算中,首先看到本文取用abs(-2.33)为99%信心水准的临界值,会使用abs()而非直接取用2.33是想提醒读者:风险值考量的是投资组合下跌风险的价值,所以用-2.33,而风险值表达通常为「正数」,因此加上绝对值。
dear = pd.DataFrame({'Mean': Mean, 'STD': STD, 'Maximum': MAX, 'Minimum': Min, '99%绝对VaR': abs_var, '99%相对VaR': re_var},index = ticker)# 直接将DEAR命名为绝对、相对VaR,供后续计算使用
rho = data2.corr() # Apply ret to avoid spurious regression result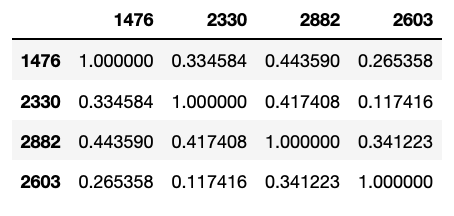
要运用报酬率资料取得标的间相关系数,而非价格资料,才能够避免假性回归导致的错误相关系数。
# 将不需用到的资料剔除。dear = dear.drop(columns = ['Mean', 'STD', 'Maximum', 'Minimum'])# 合并 dear 与 rhoportfolio = pd.concat([dear, rho,], axis = 1)portfolio[['99%绝对VaR', '99%相对VaR']] = portfolio[['99%绝对VaR', '99%相对VaR']]
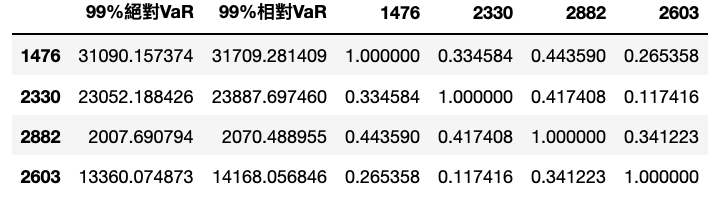
part1的部分是个别标的本身之风险值;part2则是标的间经相关系数调整的风险值。
part1 = sum(portfolio['99%绝对VaR']**2)part2 =2*portfolio.iat[0,3] * portfolio.iat[0,0] * portfolio.iat[1,0]+ 2*portfolio.iat[0,4] * portfolio.iat[0,0] * portfolio.iat[2,0]+ 2*portfolio.iat[0,5] * portfolio.iat[0,0] * portfolio.iat[3,0]+ 2*portfolio.iat[1,4] * portfolio.iat[1,0] * portfolio.iat[2,0]+ 2*portfolio.iat[1,5] * portfolio.iat[1,0] * portfolio.iat[3,0]+ 2*portfolio.iat[2,5] * portfolio.iat[2,0] * portfolio.iat[3,0]
99%信心水准之绝对风险值为50647.78。
part1 = sum(portfolio['99%相对VaR']**2)part2 =2*portfolio.iat[0,3] * portfolio.iat[0,1] * portfolio.iat[1,1]+ 2*portfolio.iat[0,4] * portfolio.iat[0,1] * portfolio.iat[2,1]+ 2*portfolio.iat[0,5] * portfolio.iat[0,1] * portfolio.iat[3,1]+ 2*portfolio.iat[1,4] * portfolio.iat[1,1] * portfolio.iat[2,1]+ 2*portfolio.iat[1,5] * portfolio.iat[1,1] * portfolio.iat[3,1]+ 2*portfolio.iat[2,5] * portfolio.iat[2,1] * portfolio.iat[3,1]
99%信心水准之相对风险值为52205.86。
根据上述的计算结果,可以推论此投资组合於单一交易日之最大损失金额有99%的机率不会超过5万2千元;然而,再经过一段时间,市场也会有所变化,因此需要再次计算风险值,才能更准确的评估部位风险。
以下将呈现投资标的之报酬率分配图,查验各标的厚尾现象的严重程度。
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS']fig, ax =plt.subplots(figsize = (18, 12), nrows = 2, ncols = 2)data2['1476'].plot.hist(ax=ax[0][0], bins = 100,range=(data2['1476'].min(), data2['1476'].max()), label = '儒鸿')ax[0][0].legend(loc = 2, fontsize = 30)data2['2330'].plot.hist(ax=ax[0][1], bins = 100,range=(data2['2330'].min(), data2['2330'].max()), label = '台积电')ax[0][1].legend(loc = 2, fontsize = 30)data2['2882'].plot.hist(ax=ax[1][0], bins = 100,range=(data2['2882'].min(), data2['2882'].max()), label = '国泰金')ax[1][0].legend(loc = 2, fontsize = 30)data2['2603'].plot.hist(ax=ax[1][1], bins = 100,range=(data2['2603'].min(), data2['2603'].max()), label = '长荣')ax[1][1].legend(loc = 2, fontsize = 30)plt.tight_layout()
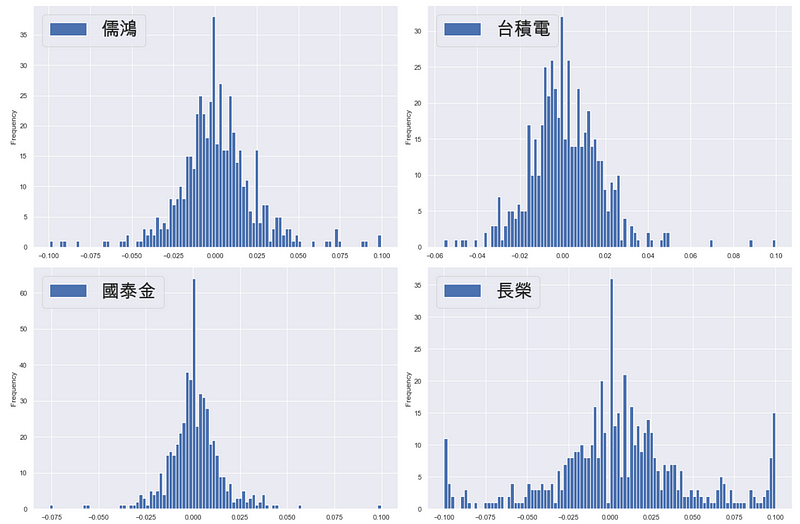
由上图可以了解,长荣的厚尾现象最为严重,而台积电与儒鸿也有厚尾的现象,国泰金则比较不明显。
根据本文前述的计算以及分析,相信读者可以明白风险值(变异数-共变异数法)的计算流程:首先,计算个别标的之每日盈余风险;接著,计算标的间相关系数;最后,计算整体投资组合的风险值。当然,在文末,本文也说明此方法的局限性,首先是针对线性证券资产;其次为「厚尾」问题,而通过图表的呈现,读者也可以了解文中四项标的资产确实具有厚尾现象,至于此问题要如何解决,请持续关注本平台,后续会有其他文章说明。最后,欢迎读者选购 TEJ E Shop中的方案,就能够轻松地对自己的投资组合进行风险值计算。

电子报订阅