效率前缘曲线

Sep 07 2021

本文重点概要

文章难度：★★★☆☆
效率前缘计算与视觉化
阅读建议：这篇文章大概介绍理论核心，并不会详细讨论，如果对理论有兴趣的读者可以查询相关文献，而在数学计算上会相对复杂，使用较多函数式编写，以增加计算效能并减少记忆体需求，在视觉化的部分使用 plotly 模组，互动式的图表让我们对结果能有更深的体会。

前言

大部分的人在决定自己的投资组合该怎么分配权重时，常常没有一个依据，而诺贝尔经济学得奖者 Harry Markowitz 提出一个理论，依据股票的波动度和彼此的相关性，根据不同的权重设定，找到一条「总风险相同时，相对上可获得最高之预期报酬率」，如此一来就可以根据自己的风险承受度去选择投资组合的权重分配了！

编辑环境及模组需求

本文使用 Mac OS 并以 Jupyter Notebook 作为编辑器

# 基础
import numpy as np
import pandas as pd
# 绘图
import matplotlib.pyplot as plt
import matplotlib
import plotly.express as px
import plotly.graph_objects as go
# API
import tejapi
tejapi.ApiConfig.api_key = 'Your Key'
tejapi.ApiConfig.ignoretz = True

资料库使用

免费资料库 : 资料库代码 ‘ TRAIL/TAPRCD ’

资料捞取

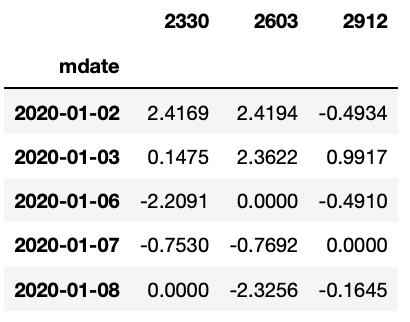
Step 1. 捞我们以台积电(2330)、长荣(2603)、统一超商(2912) 作为投资组合的范例，日期选定 2020 年度，栏位选择报酬率 roi。

data = tejapi.get('TRAIL/TAPRCD',
                  coid=['2330', '2603', '2912'],
                  mdate={'gte': '2020-01-01', 'lte': '2020-12-
                          31'},
                  opts={"sort": "mdate.desc", 'columns': [
                        'coid', 'mdate', 'roi']},
                  paginate=True)

Step 2. 重设索引值、资料转置、栏位以股票代号命名

data = data.set_index('mdate')
returns = data.pivot(columns='coid')
returns.columns = [columns[1] for columns in returns.columns]

Step 3. 计算平均报酬、共变异数矩阵

mean_returns = returns.mean()
cov_matrix = returns.cov()

投资组合计算

接下来我们要随机产生投资组合权重，利用大量模拟进而找出效率前缘，我们要针对每一个投组纪录他的报酬率、标准差、权重，我们定义两组函数。

def portfolio_performance(weights, mean_returns, cov_matrix):
    returns = np.sum(mean_returns*weights )
    std = np.sqrt(np.dot(weights.T, np.dot(cov_matrix, weights))) 
    return std, returns

我们要模拟的投资组合数量

num_portfolios = 5000

将函数在放入随机投组计算函数里，计算每一个投资组合的数据

def random_portfolios(num_portfolios, mean_returns, cov_matrix):
    results = np.zeros((3,num_portfolios))
    weights_record = []
    for i in range(num_portfolios):
        weights = np.random.random(len(coid))
        weights /= np.sum(weights)
        weights_record.append(weights)
        portfolio_std_dev, portfolio_return = 
        portfolio_performance(weights, mean_returns, cov_matrix)
        results[0,i] = portfolio_std_dev
        results[1,i] = portfolio_return
        results[2,i] = (portfolio_return) / portfolio_std_dev
    return results, weights_record

开始模拟，并将结果存入 results 和 weights_record

results = np.zeros((3,num_portfolios))
weights_record = []
for i in range(num_portfolios):
    weights = np.random.random(len(coid))
    weights /= np.sum(weights)
    weights_record.append(weights)
    portfolio_std_dev, portfolio_return = 
    portfolio_performance(weights, mean_returns, cov_matrix)
    results[0,i] = portfolio_std_dev
    results[1,i] = portfolio_return
    results[2,i] = (portfolio_return) / portfolio_std_dev

视觉化，鼠标跳出的文字框，第一个数字代表风险，第二个数字代表报酬，第二行数组代表投资的权重。

def protfolios_allocation(mean_returns, cov_matrix, 
                         num_portfolios):
    results, weights = random_portfolios(
        num_portfolios, mean_returns, cov_matrix)
        
    fig = go.Figure(data=go.Scatter(x=results[0, :], 
                                    y=results[1, :],
                                    mode='markers',
                                    text = weights_record,
                                   ))
    
    fig.update_layout(title='投资组合表现分布',
                      xaxis_title="投资组合总风险",
                      yaxis_title="预期平均报酬率",)

    fig.update_xaxes(showspikes=True,spikecolor="grey",
                     spikethickness=1, spikedash='solid')

    fig.update_yaxes(showspikes=True,spikecolor="grey",
                     spikethickness=1, spikedash='solid')

    fig.show()

效率前缘计算

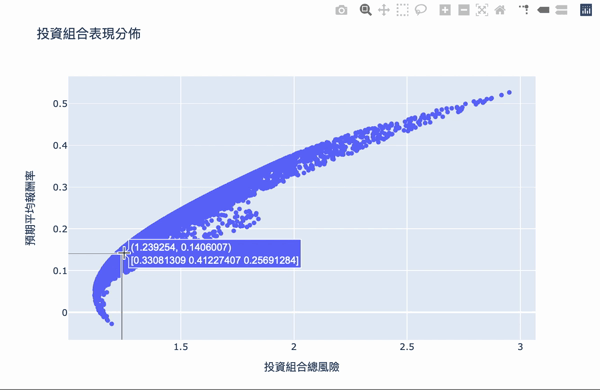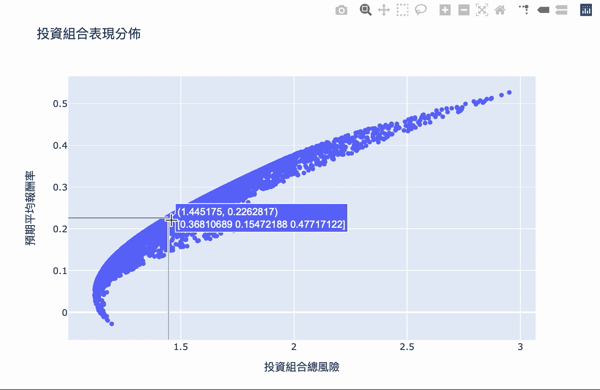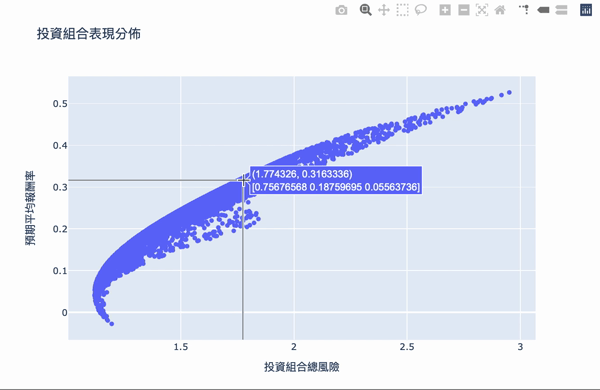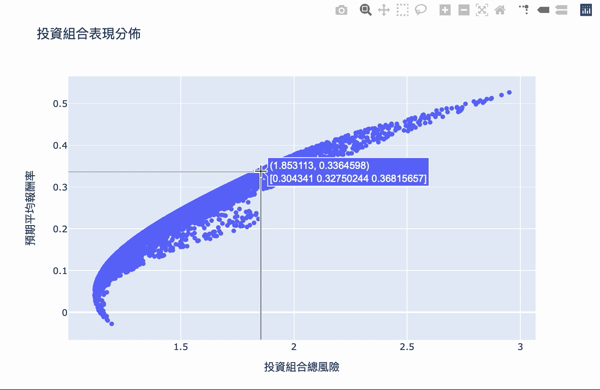
我们要找两个条件：

找出所有投资组合中最小风险的投资组合
找到相同报酬率下最小风险的投资组合

这类的条件相当于寻找极值，我们可以利用 scipy 模组下的 optimize 来计算最小值

import scipy.optimize as sco

这里定义四个计算的函数

1.风险函数

代入权重计算出报酬和标准差

def portfolio_volatility(weights, mean_returns, cov_matrix):
 return portfolio_performance(weights,mean_returns, cov_matrix)[0]

2. 风险最小投资组合

我们使用 scipy 模组下的 optimize 计算在权重 0 ～ 1 限制下，取风险函数下的极值，演算法选择 SLSQP( Sequential Least Squares Programming) 非线性规划

fun：优化的目标函数

args：目标函数可设定的参数

method：选用的优化算法

bounds：每一个x的取值范围

constraints：优化的约束条件，输入为字典组成的元组，字典主要由 ‘type‘ 和 ‘fun‘ 组成，type可选 ‘eq‘ 和 ‘ineq‘，分别是等式约束和不等式约束，fun是对应的约束条件，可为lambda函数。

def min_variance(mean_returns, cov_matrix):
    num_assets = len(mean_returns)
    args = (mean_returns, cov_matrix)
    constraints = ({'type': 'eq', 'fun': lambda x: np.sum(x) - 1})
    bound = (0,1)
    bounds = tuple(bound for asset in range(num_assets))
    result = sco.minimize(portfolio_volatility, num_assets*
             [1/num_assets,], args=args,
             method='SLSQP', bounds=bounds, 
             constraints=constraints)
    return result

3. 同报酬率下风险最小投组

主要为约束条件上的差异，报酬要限制在固定数字，求风险极小值

def efficient_return(mean_returns, cov_matrix, target):
    num_assets = len(mean_returns)
    args = (mean_returns, cov_matrix)

    def portfolio_return(weights):
        return portfolio_performance(weights, mean_returns, 
                                     cov_matrix)[1]

    constraints = ({'type': 'eq', 'fun': lambda x:  
                     portfolio_return(x) - target},
                   {'type': 'eq', 'fun': lambda x: np.sum(x) - 1})

    bounds = tuple((0,1) for asset in range(num_assets))
    result = sco.minimize(portfolio_volatility, num_assets*
                          [1/num_assets,], args=args,
                          method='SLSQP', bounds=bounds, 
                          constraints=constraints)
    return result

4. 组合效率前缘的样本

def efficient_profolios(mean_returns, cov_matrix, returns_range):
    efficients = []
    for ret in returns_range:
        efficients.append(efficient_return(mean_returns, 
                          cov_matrix, ret))
    return efficients

视觉化，方法同投组视觉化，再另外加上最小风险投组和效率前缘

结论

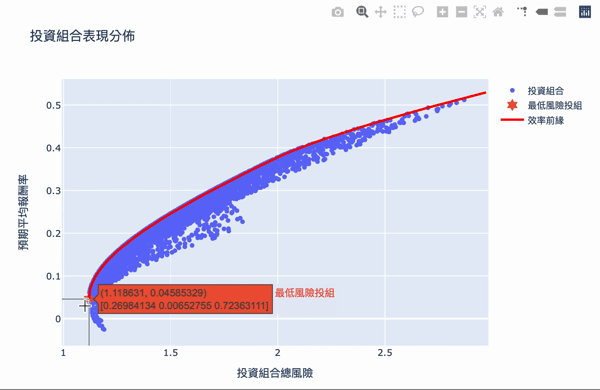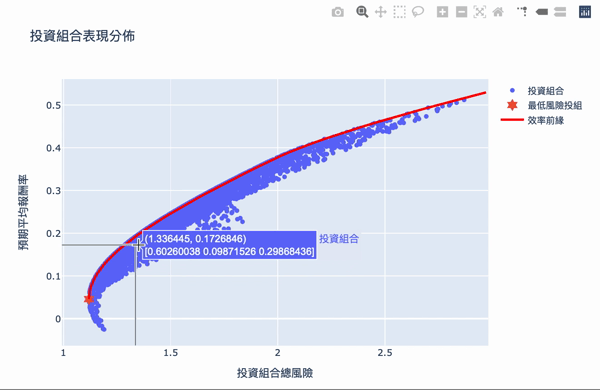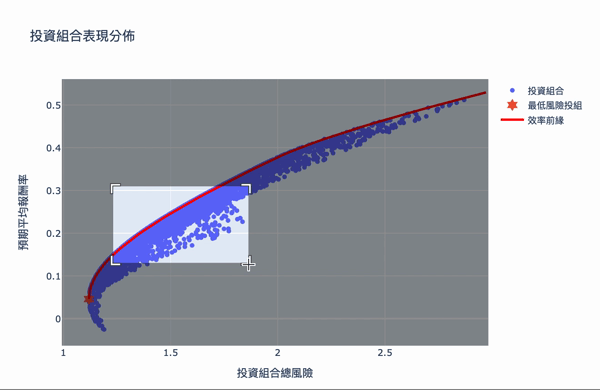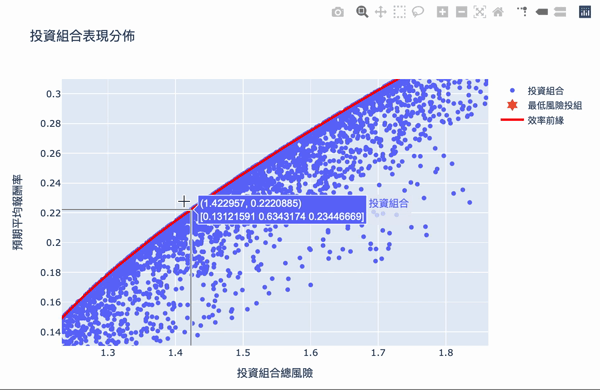
效率前缘整体架构其实不难理解，利用大量的模拟计算，求得效率的权重投资，可以设定自己想要的预期报酬，选择风险最小的投资组合，Plotly 互动式图表让我们可将鼠标移至图点上，就会显示当下投资组合的权重分配，当然万年不变的道理：「高报酬高风险」，想要更高的投资报酬率，需要承担更大的风险波动，如果对演算法有兴趣的读者，可以详阅官方文件，而此权重的结果，是根据选择资料库的时间，当时股票的波动度，所以获得的效率前缘是会随著时间不断变化，故一段时间需要调整权重分配。

完整程式码

点此连结Github