股价路径预测

Jun 02 2022

本文重点概要

文章难度：★★★☆☆
以蒙地卡罗法模拟投资组合未来走势
阅读建议：本文首先简述蒙地卡罗的方法原理，接著便会进行资料挑选、模拟过程以及结果呈现，让读者了解蒙地卡罗模拟过程的执行，文中不会提及任何数学公式，便于读者阅读。

前言

蒙地卡罗模拟法的用途是估计不确定事件的可能结果，其运作方式则是透过假设机率分布，使不确定性事件的变数建立模型。并且，每个预测期都会用一组随机数字来不断重新计算结果，借此产生大量的可能结果。

而在财务金融领域中，此方法被广泛用来衡量资产组合的报酬及风险，较注重预测末尾的极端走势。因此，本文最后也将透过视觉化结果，说明资产组合的风险报酬表现。

编辑环境及模组需求

本文使用 MacOS 并以 Jupyter Notebook 作为编辑器

＃基本套件
import numpy as np
import pandas as pd

＃绘图套件
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
sns.set()

＃TEJAPI
import tejapi
tejapi.ApiConfig.api_key = 'Your Key'
tejapi.ApiConfig.ignoretz = True

资料库使用

证券交易资料表: 资料库代码为 ‘TWN/EWPRCD’，提供证券日交易行情资讯，以及还原股价资讯。
报酬率资讯表: 资料库代码为 ‘TWN/EWPRCD2’，包含证券与指数之报日、周、月、年酬率资料。

资料处理

Step 1. 报酬率资料捞取

ticker = ['1476', '2330', '2603', '2882']
# 儒鸿, 台积电, 国泰金, 长荣

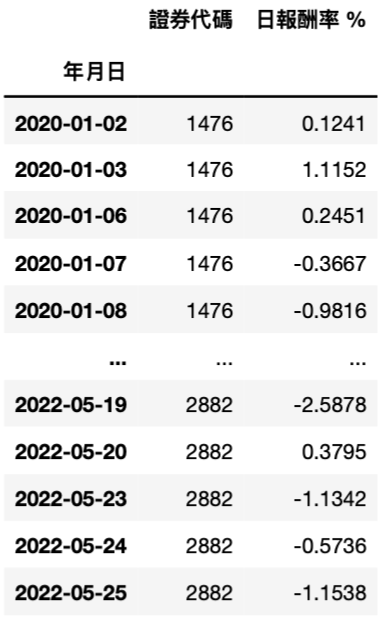
ret = tejapi.get('TWN/EWPRCD2', # 公司交易资料-已调整股价(收盘价)
                  coid = ticker,
                  mdate = {'gte':'20200101'},
                  opts = {'columns': ['coid', 'mdate', 'roia']},
                  chinese_column_name = True,
                  paginate = True)
ret = ret.set_index('年月日')

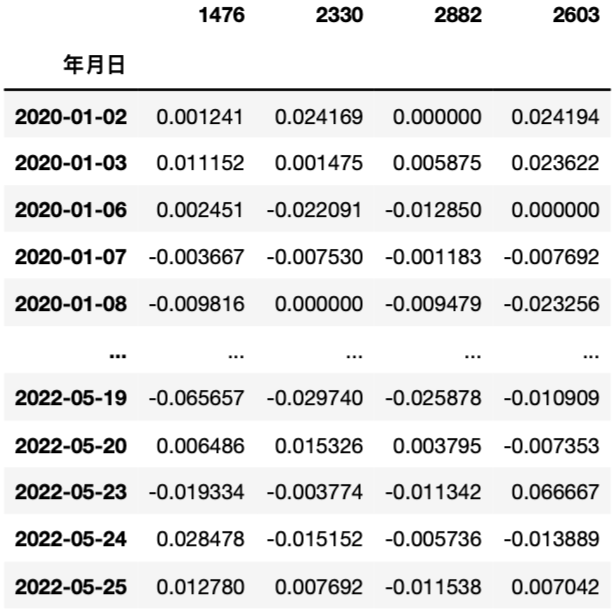
# 资料转置
RetData = {}

for i in ticker:
    r = ret[ret['证券代码'] == i]
    r = r['日报酬率 %']
    RetData.setdefault(i, r)

RetData = pd.concat(RetData, axis = 1)
RetData = RetData * 0.01

Step 2. 平均报酬、共变异数、本金计算

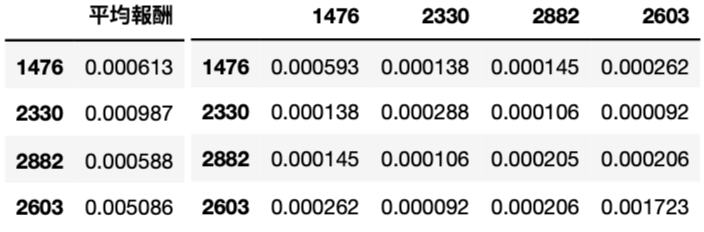
# 平均报酬
Mean = pd.DataFrame(
list(np.mean(RetData[i]) for i in RetData.columns), index=RetData.columns, columns = ['平均值'])

# 共变异数矩阵
covMatrix = RetData.cov()

price = tejapi.get('TWN/EWPRCD', # 公司交易资料-未调整股价
                  coid = ticker,
                  mdate = {'gte':'20220525', 'lte':'20220525'},
                  opts = {'columns': ['coid', 'mdate', 'close_d']},
                  chinese_column_name = True,
                  paginate = True)

price = price.set_index('年月日')
principal = (price.loc['2020-05-25']['收盘价(元)'].sum()) * 1000

透过加总四支标的于2020年5月25日的收盘价，并假设至少持有一张股票(1000股)，则初始本金为1,193,900元。

模拟条件设定

权重设定、模拟期间与模拟次数

# 权重设定
weights = list()

for i in range(4):
    weights.append(list(price['收盘价(元)'])[i]/price['收盘价(元)'].sum())

# 模拟次数
number_of_trial = 100

# 模拟期间
sim_period = 30

在权重设定的部分，读者可以根据自身标的持有情形而做改变，此处直接使用股价权重比例仅为示范而已。

儒鸿：40%、台积电：44%、长荣：12%、国泰金：4%。

模拟计算流程

sim_mean = np.full(shape = (sim_period, 4), fill_value = Mean.T.loc['平均报酬'])
sim_mean = sim_mean.T

首先，定义储存表格sim_mean并填入各标的之平均报酬，再将其转置，将个别标的独立出来。

sim_portfolio = np.full(shape = (sim_period, number_of_trial), fill_value = 0)

接著，定义储存表格sim_portfolio为投资组合的预测栏位，并先行将每个栏位填入0，后续再通过计算填入该预测路径该期间之预测值。

for i in range(0, number_of_trial):
    multi_normal = np.random.normal(size = (sim_period, 4))
    cholesky = np.linalg.cholesky(covMatrix)
    
    sim_return = sim_mean + np.inner(cholesky, multi_normal)
    
    sim_portfolio[:,i] = 
    np.cumprod(np.inner(weights, sim_return.T)+1) * principal

multi_normal:

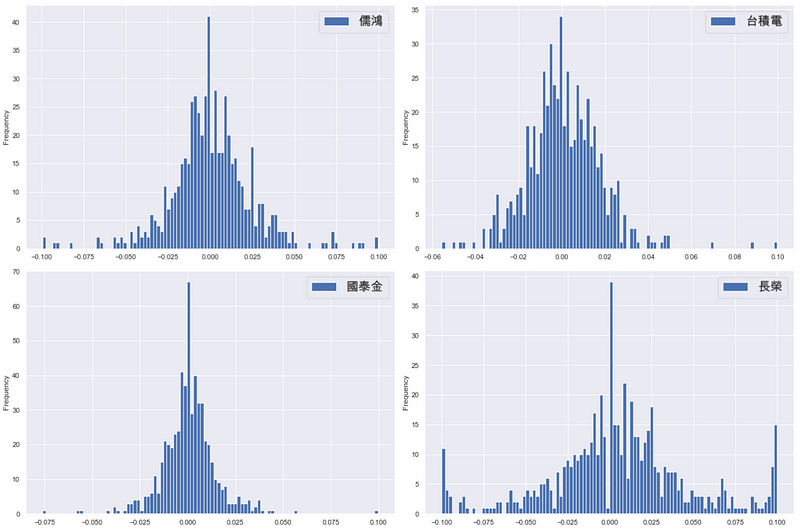
从上图中可以发现，除了长荣(2603)有较严重的厚尾问题，各项标的报酬分配大致上接近常态分配，因此本文此处也套用常态分配在各标的上。

cholesky:

在处理多资产投资组合时，透过cholesky分解出共变异数矩阵的下三角矩阵，处理标的间相关性问题。

接著，将上述两矩阵内积，得到模拟之各项标的报酬走势；最后乘上个标的权重比例(同样是内积)以及初始本金，即完成投资组合路径模拟计算。

视觉化模拟结果

plt.rcParams['font.sans-serif'] = ['Arial Unicode MS'] ＃ 输入中文plt.figure(figsize=(15,8)) ＃框定图表尺寸plt.plot(sim_portfolio)
plt.ylabel('投资组合累积价值变动', fontsize = 15)
plt.xlabel('模拟期间', fontsize = 15)
plt.title('模拟路径', fontsize = 20)
plt.show()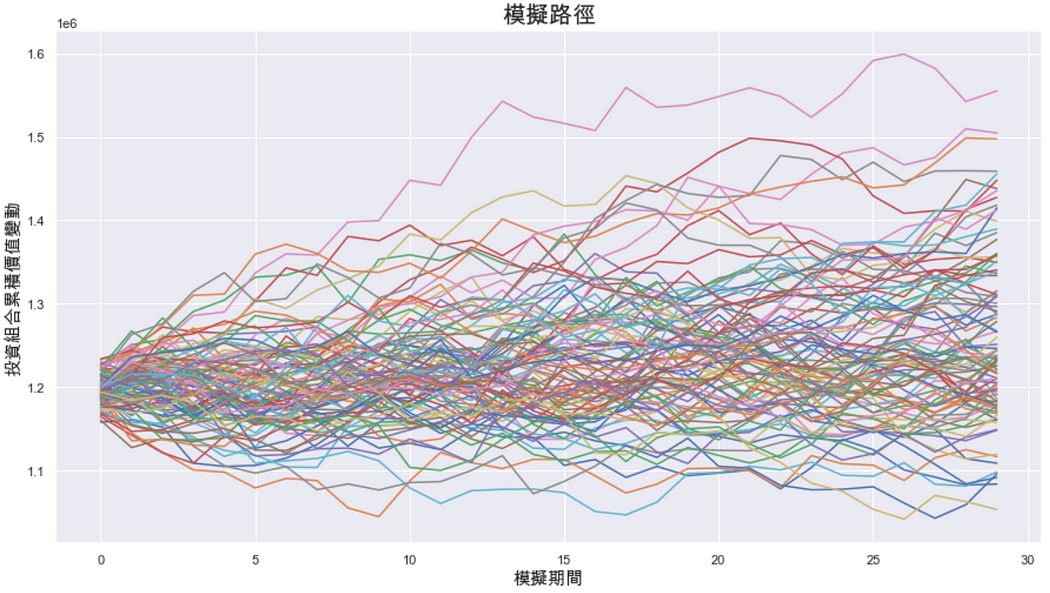

透过这一次的模拟结果，可以借由图表中最下面的路径推论，接下来一个月该投资组合走势下档风险最多不会超过 -16%；而上涨报酬最大可能为25%。因此该投资组合有较低下档风险以及较高的涨势机率。

结论

透过上述的过程，相信读者可以明白蒙地卡罗方法的执行流程，并且可以知道其背后具有统计理论的支撑；然而，也因为蒙地卡罗方法是透过随机机率为基础进行大量计算，以模拟将来的可能走势，所以不能代表市场会全然地与预测结果相同，若市场中有大幅度的波动导致极端值产生，则蒙地卡罗方法的参考性就有所降低。因此，想要在市场中保有领先地位，不仅仅要有逻辑清晰且数据支持的分析结果，也必须时刻掌握资讯的流通，而TEJ也欢迎读者选购 TEJ E Shop中的方案，相信读者具有完整的资料库后，就能轻易地完成自身资产配置的走势模拟，并掌握市场整体的脉动。

完整程式码

点此前往Github