衡量公司盈余管理程度

Dec 15 2021

本文重点概要

文章难度：★★★☆☆
特定益本比分组组别存在较高的盈余管理程度
阅读建议：本文透过比较同产业公司裁决性应计项目 Discretionary Current Accrual(DCA)来衡量个别公司盈余管理程度，若想了解更具专业性的公司信用风险模型，可进一步参考 TEJ信用风险。
完整程式码附在TEJ github

前言

盈余是投资人在意的关键指标之一，盈余高低及未来走向会影响投资人持股意愿，若投资人预期公司盈余增加，会提高持股意愿。而盈余可分为现金部分与应计项目部分，应计项目又可分为裁决性与非裁决性，公司管理层操控纵的，即为裁决性应计项目部分。根据过去研究，公司管理层有诱因透过会计原则、损益之自由裁量权等手段，来达到其拟定的盈余目标。

在投资人与公司管理层存在资讯不对称的情况下，公司管理层采用裁决性应计项目作为盈余管理的手段，投资人可能因此错估公司的真实盈余，而高估公司未来股价。故本文透过衡量每年公司盈余管理程度，可以让我们避免持有在同产业中有较高盈余管理程度的公司。

编辑环境及模组需求

本文使用 Windows OS 并以 Jupyter Notebook 作为编辑器

# 功能模组 import pandas as pd import numpy as np import statsmodels.api as sm import matplotlib.pyplot as plt from scipy.stats import wilcoxon # TEJ API import tejapi tejapi.ApiConfig.api_key = 'Your key'

资料库使用

证券属性表：资料库代码为(TWN/EWNPRCSTD)
IFRS以合并为主简表 ( 累计 ) — 全产业：资料库代码为(TWN/AIM1A)
IFRS以合并为主财务(累计)-全部产业Ⅳ_报表封面：资料库代码为(TWN/AIFINA)
上市(柜)未调整股价(日)：资料库代码为(TWN/APRCD)

资料处理

Step 1. 捞取产业代码、财务与股价资料

# 汇入 台湾交易所所有代码 code = tejapi.get("TWN/EWNPRCSTD",                   paginate=True,                   opts={'columns':['coid', 'mdate', 'stypenm','market','tseindnm']},                   chinese_column_name=True) # 汇入 财务资料 data = tejapi.get('TWN/AIM1A',                   coid = code['证券码'].tolist(),                   mdate= {'gte': '2012-01-01','lte':'2020-12-31'},                   opts={'pivot':True,                         'columns':['coid', 'mdate','0010','0130','R531',                                    '7210','3100','0400','3990']},                   chinese_column_name=True,                           paginate=True) # 汇入 财报发布日  data_annouce = tejapi.get('TWN/AIFINA',                           coid = code['证券码'].tolist(),                           mdate= {'gte': '2012-01-01','lte':'2020-12-31'},                           opts={'columns':['coid', 'mdate', 'a0003']},                           chinese_column_name=True,                           paginate=True)

股价是日频率资料，一档股票至少有千笔资料，而 TEJ为维持主机运行的稳定，系统限制单次取得最大笔数为10,000笔，可使用 paginate=True 参数分次取得资料，但总笔数单次最多为1,000,000笔。故我们可以将公司以50家分一组，以便回圈分次捞取资料。

groups = [] while True:     if len(security_list) >= 50:         groups.append(security_list[:50])         security_list = security_list[50:]     elif 0 <= len(security_list) < 50:         groups.append(security_list)         break # 汇入未调整股价 data_price = pd.DataFrame()     for group in groups:     data_price = data_price.append(tejapi.get('TWN/APRCD',                                               coid = group,                                               mdate= {'gte': '2013-03-01','lte':'2021-3-31'},                                               opts={'columns':['coid', 'mdate','close_d']},                                               chinese_column_name = True,                                               paginate = True)).reset_index(drop=True)

Step 2. 只保留三月底收盘价与年底资料

将栏位名称改成相同栏位名称，以便合并不同 Dataframe时，不会重复出现相同栏位名称。因为益本比的分母限定是每年三月底收盘价，故data_price只需要保留三月底股价资料，data 也只需要保留年底资料。

# 资料前处理 code = code.rename({'证券码': '公司'}, axis=1) # 改名字 data = data.rename({'公司代码':'公司'}, axis=1) # 改名字 data_annouce = data_annouce.rename({'年/月':'财报年月'}, axis=1) # 改名字 data_price = data_price.rename({'证券代码':'公司'}, axis=1) # 改名字 data_price['年'] = data_price['年月日'].dt.year - 1 # 改成财报年 data_price = data_price[data_price['年月日'].dt.month == 3] data_price = data_price.drop_duplicates(subset=['公司','年'], keep='last') # 只保留三月底收盘价 data['年'] = data['财报年月'].dt.year data = data.drop_duplicates(subset=['公司','年'], keep='last') # 只保留年底资料

Step 3. 合并不同资料库资料

# 合并资料
data = data.merge(code[['TSE产业名','公司']] ,how = 'left' ,on=['公司']) 
data = data.merge(data_annouce,how = 'left' ,on=['公司','财报年月'])
data = data.merge(data_price[['公司','年','收盘价(元)']] ,how = 'left' ,on=['公司','年'])

将财报发布日与三月底股价资料合并至同一个dataframe中。

计算 DCA与益本比分组

Step 1. 准备 DCA所需的财务资料

本文采用 Jones(1991)模型，Jones(1991)研究认为应计项目中，受到经济环境影响的部分与销货有关；折旧性资产毛额与总应计项目中之非裁决性折旧费用有关。同时，因为产业有商业模式的差异；公司有规模的差异，所以我们应该进一步考量产业差异与公司规模。故我们要先整理上述提及的财务资料。

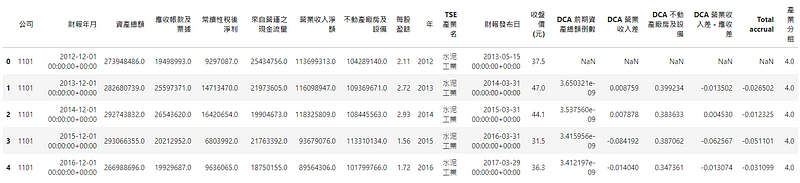
# 计算 DCA  data['Total accrual'] = (data['常续性税后净利'] - data['来自营运之现金流量']) * data['DCA 前期资产总额倒数'] # Y data['DCA 前期资产总额倒数'] = 1 / data.groupby('公司')['资产总额'].shift(1) # X0 data['DCA 营业收入差'] = data.groupby('公司')['营业收入净额'].diff() * data['DCA 前期资产总额倒数'] # X1 data['DCA 不动产厂房及设备'] = data['不动产厂房及设备'] * data['DCA 前期资产总额倒数'] # X2 data['DCA 营业收入差 - 应收差'] = (data.groupby('公司')['营业收入净额'].diff() -                             data.groupby('公司')['应收帐款及票据'].diff()) * data['DCA 前期资产总额倒数'] # X1

透过产业分组回归，排除产业差异，同时将相似产业分于同组，避免单一产业家数过少，回归产生不可靠的统计数字；透过前期总资产平减，排除公司规模差异。

# 分组相似产业 data['产业分组'] =      np.select([(data['TSE产业名'].isin(["食品工业","纺织纤维","造纸工业"])) ,                (data['TSE产业名'].isin(["塑胶工业","橡胶工业","化学工业","油电燃气业"])),                (data['TSE产业名'].isin(["汽车工业","钢铁工业"])),                (data['TSE产业名'].isin(["电机机械","电器电缆"])),                (data['TSE产业名'].isin(["水泥工业","建材营造","玻璃陶瓷"])),                (data['TSE产业名'].isin(["资讯服务业","电子商务","贸易百货"])),                (data['TSE产业名'].isin(["观光事业","航运业","文化创意业"])),                (data['TSE产业名'].isin(["生技医疗"])),                (data['TSE产业名'].isin(["光电业"])),                (data['TSE产业名'].isin(["半导体"])),                (data['TSE产业名'].isin(["电脑及周边"])),                (data['TSE产业名'].isin(["通信网路业"])),                (data['TSE产业名'].isin(["电子零组件"])),                (data['TSE产业名'].isin(["其他电子业","电子通路业","农业科技","其他"]))],               list(range(14)), default = np.nan)

Step 2. 分年与产业计算 DCA

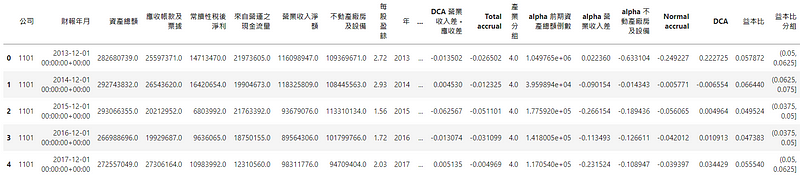
设定资产总额、营业收入与不动产厂房及设备为解释变数，应计数字为被解释变数，透过逐年回归同产业的财务资料，可获得每家公司应计数字的回归模型观察值与实际值，而实际值-观察值的差额便是 DCA，若 DCA大于0，则表示该公司盈余管理程度大于公司所属产业。

# 计算 DCA def regress(data):     '''     每年不同产业分组跑回归，主要用来获得回归系数     '''     data = data[['Total accrual','DCA 前期资产总额倒数','DCA 营业收入差','DCA 不动产厂房及设备']].dropna()     Y = data['Total accrual']     X = data[['DCA 前期资产总额倒数','DCA 营业收入差','DCA 不动产厂房及设备']]     X = X.rename(columns={"DCA 前期资产总额倒数": "alpha 前期资产总额倒数",                           "DCA 营业收入差": "alpha 营业收入差",                           "DCA 不动产厂房及设备": "alpha 不动产厂房及设备",})     try:         result = sm.OLS(Y, X).fit()         return result.params     except ValueError:           pass data = data.merge(data.groupby(['财报年月','产业分组']).apply(regress).reset_index(),                         how = 'left' ,on = ['财报年月','产业分组']) data['Normal accrual'] = (data['alpha 前期资产总额倒数'] * data['DCA 前期资产总额倒数']                            + data['alpha 营业收入差'] * data['DCA 营业收入差 - 应收差']                                + data['alpha 不动产厂房及设备'] * data['DCA 不动产厂房及设备']) data['DCA'] = data['Total accrual'] - data['Normal accrual']

Step 3. 益本比分组

将全部公司以益本比 Earnings-Price Ratio来分组，可进一步判断是否特定益本比范围内的公司有没有异常的盈余管理程度。

# 计算益本比，并以0.0125分组。 def cal_EP_label():     '''获得 EP ratio分组下的公司数，num=33，切0.025'''     label = np.linspace(-0.2, 0.2, num=33).tolist()     label = [ '%.4f' % elem for elem in label ]     label.insert(0,-np.inf)     label.insert(len(label),np.inf)     label = np.array(label, dtype=float)     return label data['益本比'] = data['每股盈余'] / data['收盘价(元)'] data['益本比分组'] = pd.cut(data['益本比'],bins = cal_EP_label() ,right=True)

视觉化结果

Step 1. 做图观察益本比分布状况

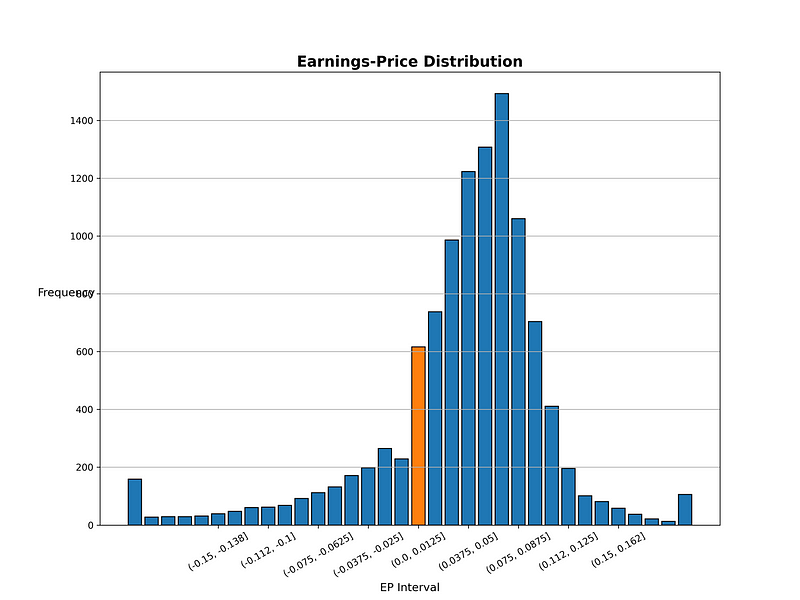
下图益本比分布落在(-0.0125, 0.0]与(0.0, 0.0125]的公司数有显著的差异，这是否表明在此益本比范围内的公司管理层面对盈余亏损时，存在损失趋避行为，因为亏损不好向股东交代，而操弄盈余管理，使每股盈余由负转正。

#%% 做图 观察益本比分组状况 fig = plt.figure(figsize = (12,9)) ax = fig.add_subplot() factor = data.groupby(['益本比分组'])['公司'].count().reset_index()['益本比分组'].astype(str) value = data.groupby(['益本比分组'])['公司'].count().reset_index()['公司'] ax.bar(factor,value,fill = '#eb3434',edgecolor = 'black') ax.bar('(0.0, 0.0125]',value[17],fill = '#eb344f',edgecolor = 'black') ax.set_title('Earnings-Price Distribution',               fontsize=16,               fontweight='bold') ax.set_xticks(['(-0.15, -0.138]','(-0.112, -0.1]','(-0.075, -0.0625]','(-0.0375, -0.025]','(0.0, 0.0125]',               '(0.0375, 0.05]','(0.075, 0.0875]','(0.112, 0.125]','(0.15, 0.162]']) plt.grid(axis='y') plt.xticks(rotation=30) plt.xlabel('EP Interval',fontsize=12) plt.ylabel('Frequency',fontsize=12, rotation=0) plt.show()

Step 2. 做表观察益本比分组与盈余管理程度关系

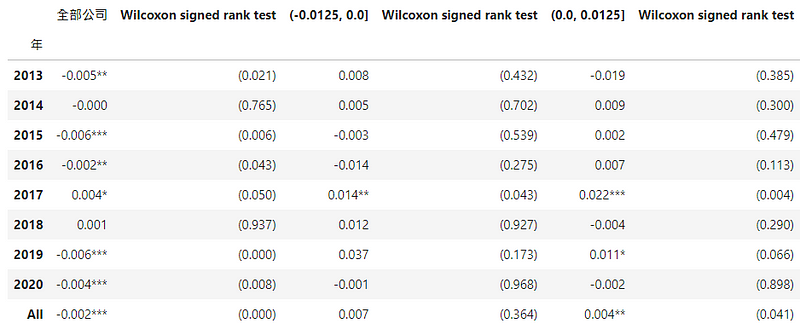
对益本比分组分别进行威尔卡森符号检定 (Wilcoxon signed-rank test)的中位数检定，发现全部公司 DCA的中位数为-0.002，且显著不为0，而益本比落在(-0.0125, 0.0]与(0.0, 0.0125]范围的公司，其 DCA 中位数为0.004，且(0.0, 0.0125]显著不为0，可以得知益本比落在(0.0, 0.0125]的公司普遍存在盈余管理。

def cal_wilcoxon(group):     return pd.DataFrame({'DCA': group.median(),                          'p-value': wilcoxon(group)[1]}, index = [0]) def add_star(df,p_value):     '''     p-values of the Wilcoxon signed rank test <= 0.01，则系数新增***     0.01 < p-values of the Wilcoxon signed rank test <= 0.05，则系数新增**     0.1 < p-values of the Wilcoxon signed rank test <= 0.01，则系数新增*     '''     df = np.select([(p_value <= 0.01),                       (p_value > 0.01) & (p_value <= 0.05),                       (p_value > 0.05) & (p_value <= 0.1)],                      [df.apply(lambda x: '%.3f'%x + '***'),                       df.apply(lambda x: '%.3f'%x + '**'),                       df.apply(lambda x: '%.3f'%x + '*')],                      default = df.apply(lambda x: '%.3f'%x))     return dfdef run_data_cal_wilcoxon(df):     '''p-values of the Wilcoxon signed rank test for one sample median DCA equal to 0'''     finaldf = pd.DataFrame()     for data in df:         temp = data.dropna(subset=['DCA']).groupby('年')['DCA'].             apply(cal_wilcoxon).reset_index(level=1, drop=True)         temp.loc['All','DCA'] = data.dropna(subset=['DCA'])['DCA'].median()         temp.loc['All','p-value'] = wilcoxon(data.dropna(subset=['DCA'])['DCA'])[1]         temp['DCA'] = add_star(temp['DCA'],temp['p-value'])         temp['p-value'] = temp['p-value'].apply(lambda x: '(' + '%.3f'%x + ')')         finaldf = pd.concat([finaldf, temp], axis=1)        return finaldf Table = run_data_cal_wilcoxon([data,                                data[data['益本比分组'].astype(str).isin(['(-0.025, 0.0]'])],                                data[data['益本比分组'].astype(str).isin(['(0.0, 0.025]'])]])

结论

在损失趋避行为普遍存在下，人面对损失比对收益更敏感，所以公司管理层面对小亏损时，有极高的诱因透过裁决性应计项目（Discretionary Accruals）来操弄盈余管理，使每股盈余由负转正，来满足股东与资本市场的期待。

本文透过逐年衡量公司与产业的盈余管理程度，我们可以一次找出明显高于产业平均的公司，以及发现益本比落在(-0.0125, 0.0]与(0.0, 0.0125]范围内的公司存在较高的盈余管理程度。

完整程式码

点此前往Github