双因子权重设置

本文重点概要

• 文章难度：★★★★☆
• 等权重法与 IC权重法对本次回测的分组绩效并没有显著差异。
• 阅读建议：在优化多因子权重前，应该先对单因子进行分层回测与横断面回归分析，来检验单因子是否具有获利性、稳定性与可解释性，在深入研究多因子时，方能找出最具综效的因子组合。故本文参考叶怡成【台股研究室】一书，选用股东权益报酬率与股价净值比来分析权重设置对因子投组的影响。
• 完整程式码附在 TEJ github

前言

常见的权重设置是等权重与市值比权重，前者将所有因子视为相同，赋予不同因子等权重，并合成新的因子值；后者则是先在个别因子内以市值比加权合成新的因子值，再赋予不同因子等权重，再合成新的因子值，然而两种方式皆没有考虑因子的有效性。

本文考虑因子有效性，新增 IC权重法，回归个别因子对往后滚动持有报酬率的相关系数，获得 IC数值，若 IC数值高，则代表该因子当下较具有效性，在每月初动态调整因子权重时，赋予 IC数值较高的因子有较高权重。

编辑环境及模组需求

本文使用 Windows OS 并以 Jupyter Notebook 作为编辑器

#功能与视觉化模组 import pandas as pd from scipy import stats from collections import OrderedDict import matplotlib.pyplot as plt import copy #TEJ import tejapi tejapi.ApiConfig.api_key = 'Your Key' tejapi.ApiConfig.ignoretz = True

资料库使用

• ROE(A)－税后：资料库代码为(TWN/AIFIN)
• 财报发布日：资料库代码为(TWN/AIFINA)
• 上市公司除权息调整开盘价、收盘价与股价净值比：资料库代码为(TWN/APRCD1)

资料处理

Step 1. ROE、财报发布日、股价净值比与股价资料捞取

# 捞取上市所有普通股证券代码 code = tejapi.get("TWN/EWNPRCSTD", paginate=True, chinese_column_name=True) code = code["证券码"][(code["证券种类名称"] == "普通股") & (code["上市别"].isin(["TSE"]))].to_list() # 汇入 ROE变数 data_ROE = tejapi.get('TWN/AIFIN',                       coid = code,                       mdate= {'gte': '2019-01-01','lte':'2020-12-31'},                       opts={'pivot':True ,'columns':['coid', 'mdate', 'R103']},                       chinese_column_name=True,                       paginate=True) # 汇入 财报发布日 data_annouce = tejapi.get('TWN/AIFINA',                           coid = code,                           mdate= {'gte': '2019-01-01','lte':'2020-12-31'},                           opts={'columns':['coid', 'mdate', 'a0003']},                           chinese_column_name=True,                           paginate=True) # 汇入 调整后开盘价、收盘价与股价净值比 data_PB_price = tejapi.get('TWN/APRCD1',                            coid = code,                            mdate= {'gte': '2019-03-01','lte':'2020-03-31'},                            opts={'columns':['coid', 'mdate','open_adj','close_adj','pbr_tej']},                            chinese_column_name=True,                            paginate=True)

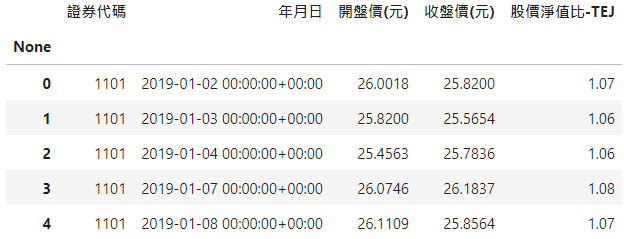
先捞取所有上市公司代码，在使用 TEJ API到不同资料库中一次捞取全部公司财务资料。

Step 2. 资料前处理

# 整理股价 data_PB_price = data_PB_price.rename({'证券代码': '公司'}, axis=1) # 改名字 data_PB_price['开盘价(元) t+1'] = data_PB_price.groupby('公司')['开盘价(元)'].shift(-1) # 新增年与月 data_PB_price['年'] = data_PB_price['年月日'].dt.year data_PB_price['月'] = data_PB_price['年月日'].dt.month data_PB_price = data_PB_price.sort_values(by=['年月日']).reset_index(drop=True) # 排序年月日

Step 3. 合并不同资料频率与筛选月底资料

# 合并季频率 ROE与财报发布日 data_all = pd.merge(data_ROE ,data_annouce ,how = 'left' , on = ['公司','年/月']) data_all = data_all.rename({'年/月': '财报'}, axis=1) # 改名字 data_all = data_all.sort_values(by=['财报发布日']).reset_index(drop=True) # 排序财报发布日 # 合并季频率与日频率资料 data_all = pd.merge_asof(data_PB_price ,data_all ,left_on = '年月日', right_on = '财报发布日', by = ['公司'] ,direction = "backward") # 留下每月底资料 data_all = data_all.drop_duplicates(subset=['公司','年','月'], keep='last') data_all = data_all.sort_values(by=['公司','年月日']).reset_index(drop=True) data_all['月持有报酬率'] = data_all.groupby('公司')['收盘价(元)'].shift(-1).reset_index(drop=True)      / data_all['开盘价(元) t+1'] -1

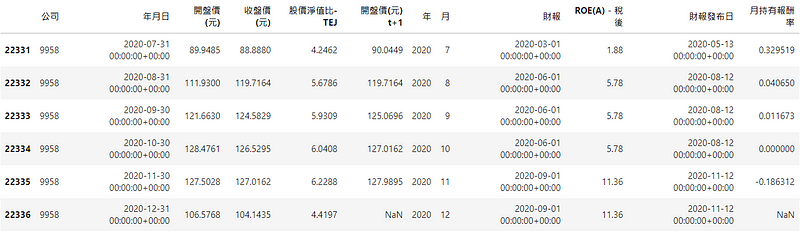
pd.merge 与 pd.merge_asof 是合并 dataframe很好用的工具，前者是合并相同频率资料，而后者是合并不同频率资料，透过参数 direction = backward可避免资料前视偏误；pd.drop_duplicates 则是可以筛选年月，保留各公司每月底的资料，方便我们获得当下准确的因子值，以利因子排序分组。

Step 4. 删除缺失值

data_all = data_all.dropna().reset_index(drop=True) data_all = data_all.set_index(['年月日','公司']) data_all = data_all[['股价净值比-TEJ','ROE(A)－税后','月持有报酬率']]

计算 IC值与建立投组

Step 1. 排序个别因子

def get_rank(data):     factors_name=[i for i in data.columns.tolist() if i not in ['月持有报酬率']] # 得到因子名     rank_df = []     for factor in factors_name:         if factor in ['股价净值比-TEJ']:             rank_list = data[factor].groupby(level=0).rank(ascending = True) # rank由小到大排序，即值越小，排名越靠前         else:             rank_list = data[factor].groupby(level=0).rank(ascending = False) # rank由大到小排序，即值越大，排名越靠前         rank_df.append(rank_list)     rank_df = pd.concat(rank_df, axis=1)     return rank_df

基于获利性概念的 ROE，越大越有高期望报酬率，故由大到小排列，即值越大，排名越靠前；基于价值股概念的股价净值比，越小越有高期望报酬率，故由小到大排列，即值越小，排名越靠前。

Step 2. 获得 IC数值

def get_ic(data):     factors_name=[i for i in data.columns.tolist() if i not in ['月持有报酬率']] # 得到因子名     ic = data.groupby(level=0).         apply(lambda data: [stats.spearmanr(data[factor],                                             data['月持有报酬率'])[1] for factor in factors_name])     ic = pd.DataFrame(ic.tolist(), index=ic.index, columns=factors_name)     return ic

IC 全名为 Information Coefficient，说明在某横断面时间下，因子对往后持有报酬率的相关系数，当下 IC值越高，表示未来持有期望报酬越高， IC 可用来比较不同因子的有效性。

Step 3. 合成新的因子值

# 根据IC计算因子权重 def ic_weight(data):     data_= data.copy()     ic = get_ic(data)       ic0 = ic.abs() # 计算 IC绝对值     rolling_ic = ic0.rolling(12,min_periods=1).mean()  # 滚动 12个月     weight = rolling_ic.div(rolling_ic.sum(axis=1),axis=0)  # 计算 IC权重,按行求和,按列相除     ranks = get_rank(data)   # 得到各因子的排序数据     score_ = OrderedDict()     for date in weight.index.tolist():         rank = ranks.loc[date]         score = rank * weight.loc[date]          score_[date] = score.sum(axis=1).to_frame().rename(columns={0: 'score'})     score_df = pd.concat(score_.values(),keys=score_.keys())     score_df = score_df.reset_index().rename({'level_0': '年月日'}, axis=1)     score_df = score_df.set_index(['年月日','公司'])     data_ = data_.join(score_df)     data_ = data_.reset_index()     return data_ data_ic = ic_weight(data_all) data_ic['因子每年分组'] = data_ic.groupby('年月日')['score'].rank().     transform(lambda x: pd.qcut(x, 10, labels = range(1,11)))

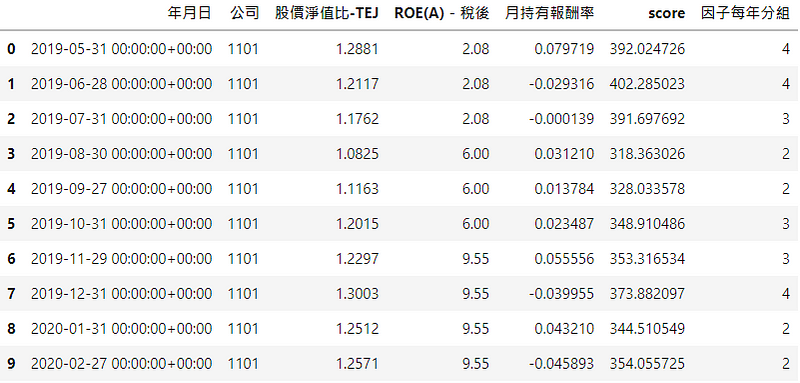
将排序后因子乘上因子 IC值权重，即各因子平均 IC值在所有因子平均 IC值加总中的占比，让 IC值大的因子有高的权重，再合成新的score因子值，由小到大排序分成 10组。

视觉化分组结果

Step 1. 计算投组逐月绩效

def arrange_group_return(tempt):     tempt = tempt.groupby(['年月日','因子每年分组'])[['月持有报酬率']].mean().reset_index()     tempt['月持有报酬率'] = tempt['月持有报酬率'] * 100     tempt = pd.pivot_table(tempt, values='月持有报酬率', index=['因子每年分组'] ,columns=['年月日'])     tempt.index = tempt.index.astype(str)     tempt = tempt.T     tempt = tempt.cumsum().dropna()     tempt.index = tempt.index.astype(str).str[:7]     return tempt data_ic = arrange_group_return(data_ic) data_ic.round(2)

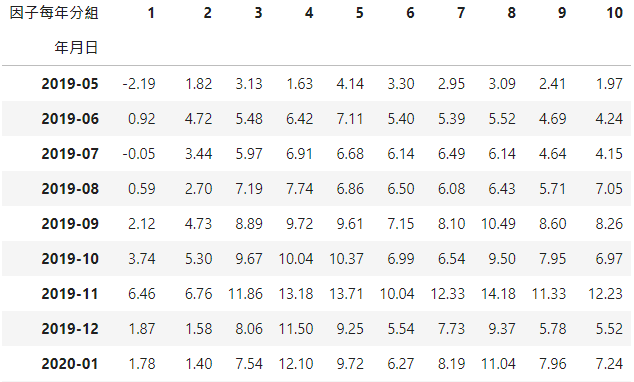
Step 2. 资料前处理

# 整理股价
data_PB_price = data_PB_price.rename({'证券代码': '公司'}, axis=1) # 改名字
data_PB_price['开盘价(元) t+1'] = data_PB_price.groupby('公司')['开盘价(元)'].shift(-1)# 新增年与月
data_PB_price['年'] = data_PB_price['年月日'].dt.year
data_PB_price['月'] = data_PB_price['年月日'].dt.month
data_PB_price = data_PB_price.sort_values(by=['年月日']).reset_index(drop=True) # 排序年月日

Step 3. 合并不同资料频率与筛选月底资料

# 合并季频率 ROE与财报发布日
data_all = pd.merge(data_ROE ,data_annouce ,how = 'left' , on = ['公司','年/月'])
data_all = data_all.rename({'年/月': '财报'}, axis=1) # 改名字
data_all = data_all.sort_values(by=['财报发布日']).reset_index(drop=True) # 排序财报发布日# 合并季频率与日频率资料
data_all = pd.merge_asof(data_PB_price ,data_all ,left_on = '年月日', right_on = '财报发布日', by = ['公司'] ,direction = "backward")# 留下每月底资料
data_all = data_all.drop_duplicates(subset=['公司','年','月'], keep='last')
data_all = data_all.sort_values(by=['公司','年月日']).reset_index(drop=True)
data_all['月持有报酬率'] = data_all.groupby('公司')['收盘价(元)'].shift(-1).reset_index(drop=True) 
    / data_all['开盘价(元) t+1'] -1

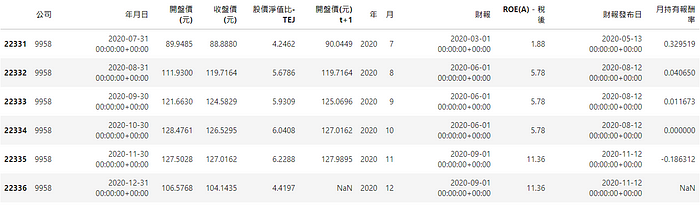
pd.merge 与 pd.merge_asof 是合并 dataframe很好用的工具，前者是合并相同频率资料，而后者是合并不同频率资料，透过参数 direction = backward可避免资料前视偏误；pd.drop_duplicates 则是可以筛选年月，保留各公司每月底的资料，方便我们获得当下准确的因子值，以利因子排序分组。

Step 4. 删除缺失值

data_all = data_all.dropna().reset_index(drop=True)
data_all = data_all.set_index(['年月日','公司'])
data_all = data_all[['股价净值比-TEJ','ROE(A)－税后','月持有报酬率']]

计算 IC值与建立投组

Step 1. 排序个别因子

def get_rank(data):
    factors_name=[i for i in data.columns.tolist() if i not in ['月持有报酬率']] # 得到因子名
    
    rank_df = []
    for factor in factors_name:
        if factor in ['股价净值比-TEJ']:
            rank_list = data[factor].groupby(level=0).rank(ascending = True) # rank由小到大排序，即值越小，排名越靠前
        else:
            rank_list = data[factor].groupby(level=0).rank(ascending = False) # rank由大到小排序，即值越大，排名越靠前
        
        rank_df.append(rank_list)
        
    rank_df = pd.concat(rank_df, axis=1)
    return rank_df

基于获利性概念的 ROE，越大越有高期望报酬率，故由大到小排列，即值越大，排名越靠前；基于价值股概念的股价净值比，越小越有高期望报酬率，故由小到大排列，即值越小，排名越靠前。

Step 2. 获得 IC数值

def get_ic(data):
    factors_name=[i for i in data.columns.tolist() if i not in ['月持有报酬率']] # 得到因子名
    ic = data.groupby(level=0).
        apply(lambda data: [stats.spearmanr(data[factor],
                                            data['月持有报酬率'])[1] for factor in factors_name])
        
    ic = pd.DataFrame(ic.tolist(), index=ic.index, columns=factors_name)
    return ic

IC 全名为 Information Coefficient，说明在某横断面时间下，因子对往后持有报酬率的相关系数，当下 IC值越高，表示未来持有期望报酬越高， IC 可用来比较不同因子的有效性。

Step 3. 合成新的因子值

# 根据IC计算因子权重
def ic_weight(data):
    data_= data.copy()
    ic = get_ic(data)  
    ic0 = ic.abs() # 计算 IC绝对值
    rolling_ic = ic0.rolling(12,min_periods=1).mean()  # 滚动 12个月
    weight = rolling_ic.div(rolling_ic.sum(axis=1),axis=0)  # 计算 IC权重,按行求和,按列相除
    ranks = get_rank(data)   # 得到各因子的排序数据
    
    score_ = OrderedDict()
    for date in weight.index.tolist():
        rank = ranks.loc[date]
        score = rank * weight.loc[date] 
        score_[date] = score.sum(axis=1).to_frame().rename(columns={0: 'score'})
    
    score_df = pd.concat(score_.values(),keys=score_.keys())
    score_df = score_df.reset_index().rename({'level_0': '年月日'}, axis=1)
    score_df = score_df.set_index(['年月日','公司'])
    data_ = data_.join(score_df)
    data_ = data_.reset_index()
    return data_data_ic = ic_weight(data_all)
data_ic['因子每年分组'] = data_ic.groupby('年月日')['score'].rank().
    transform(lambda x: pd.qcut(x, 10, labels = range(1,11)))

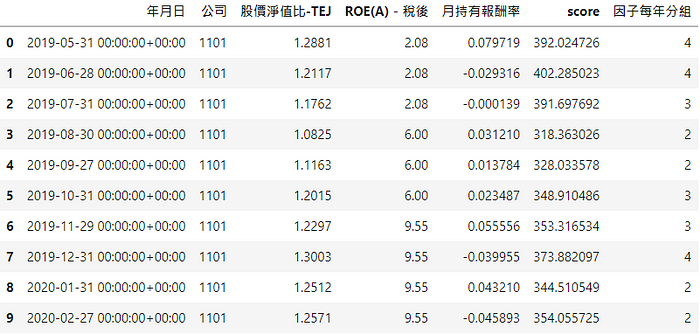
将排序后因子乘上因子 IC值权重，即各因子平均 IC值在所有因子平均 IC值加总中的占比，让 IC值大的因子有高的权重，再合成新的score因子值，由小到大排序分成 10组。

视觉化分组结果

Step 1. 计算投组逐月绩效

def arrange_group_return(tempt):
    tempt = tempt.groupby(['年月日','因子每年分组'])[['月持有报酬率']].mean().reset_index()
    tempt['月持有报酬率'] = tempt['月持有报酬率'] * 100
    tempt = pd.pivot_table(tempt, values='月持有报酬率', index=['因子每年分组'] ,columns=['年月日'])
    tempt.index = tempt.index.astype(str)
    tempt = tempt.T
    tempt = tempt.cumsum().dropna()
    tempt.index = tempt.index.astype(str).str[:7]
    
    return temptdata_ic = arrange_group_return(data_ic)data_ic.round(2)

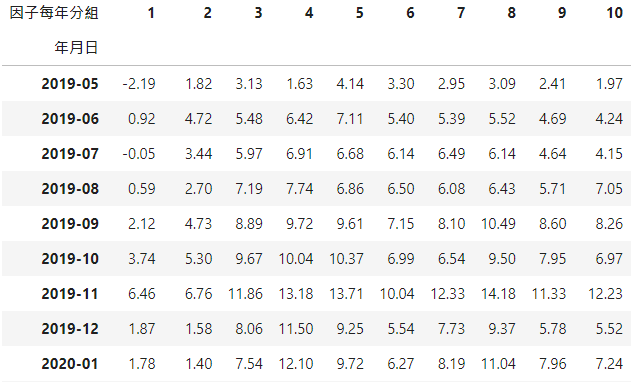
Step 2. 视觉化投组累积绩效

def draw_group_return(tempt ,weight_method):
    fig = plt.figure(figsize = (14,7))
    ax = fig.add_subplot()
    
    ax.set_title(weight_method, 
                 fontsize=16, 
                 fontweight='bold')
    
    for i in tempt.columns:
        ax.plot(tempt[i], linewidth=2, alpha=0.8 , marker='o')
    
    ax.legend(tempt.columns,loc=2)
    
    plt.grid(axis='y')
    plt.xlabel('日期', fontsize=18)
    plt.ylabel('报酬率 %',rotation=0, fontsize=18,labelpad=20)
    plt.xticks(fontsize=12)
    plt.yticks(fontsize=12)
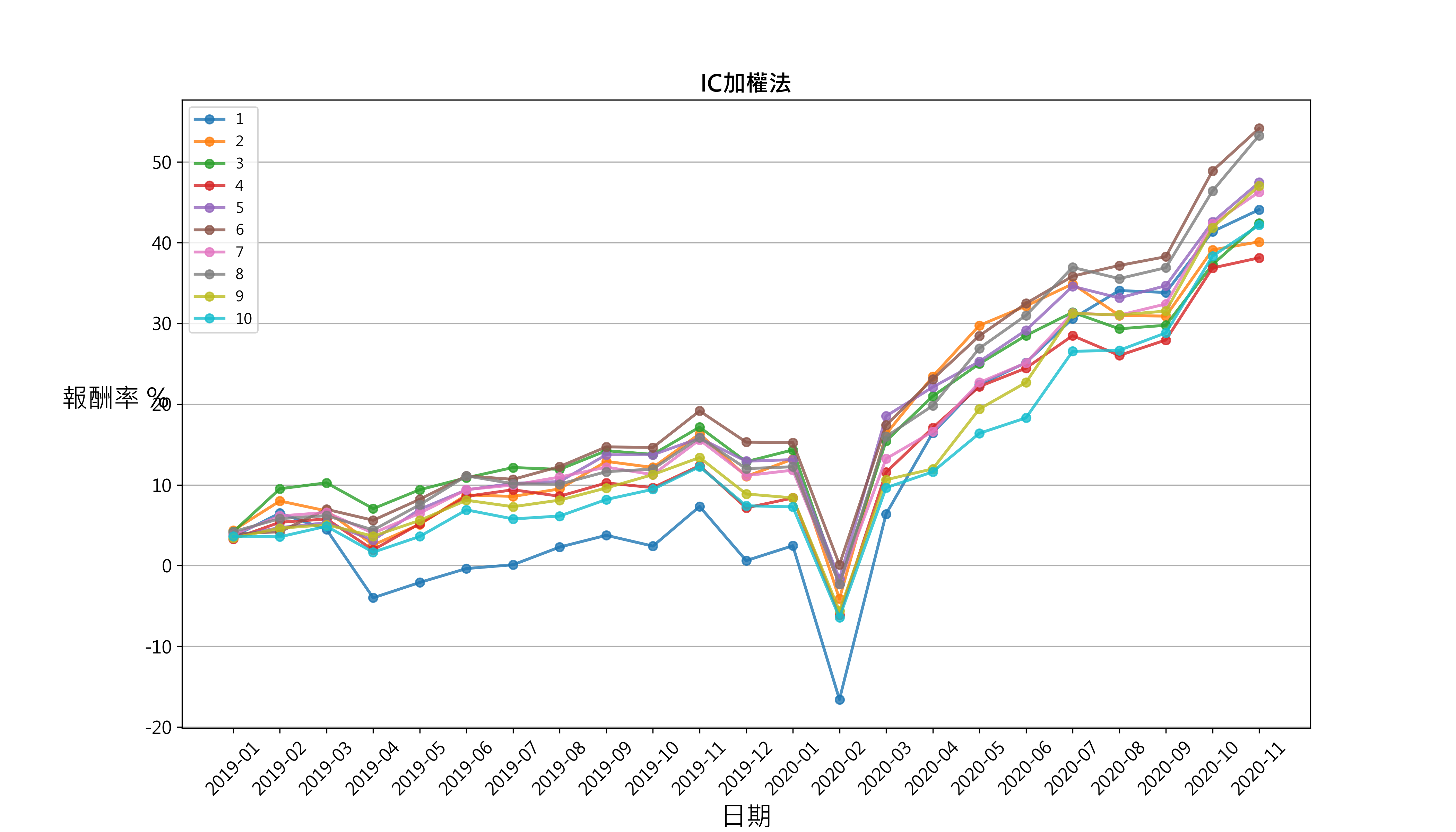
    plt.show()draw_group_return(data_ic, 'IC加权法')

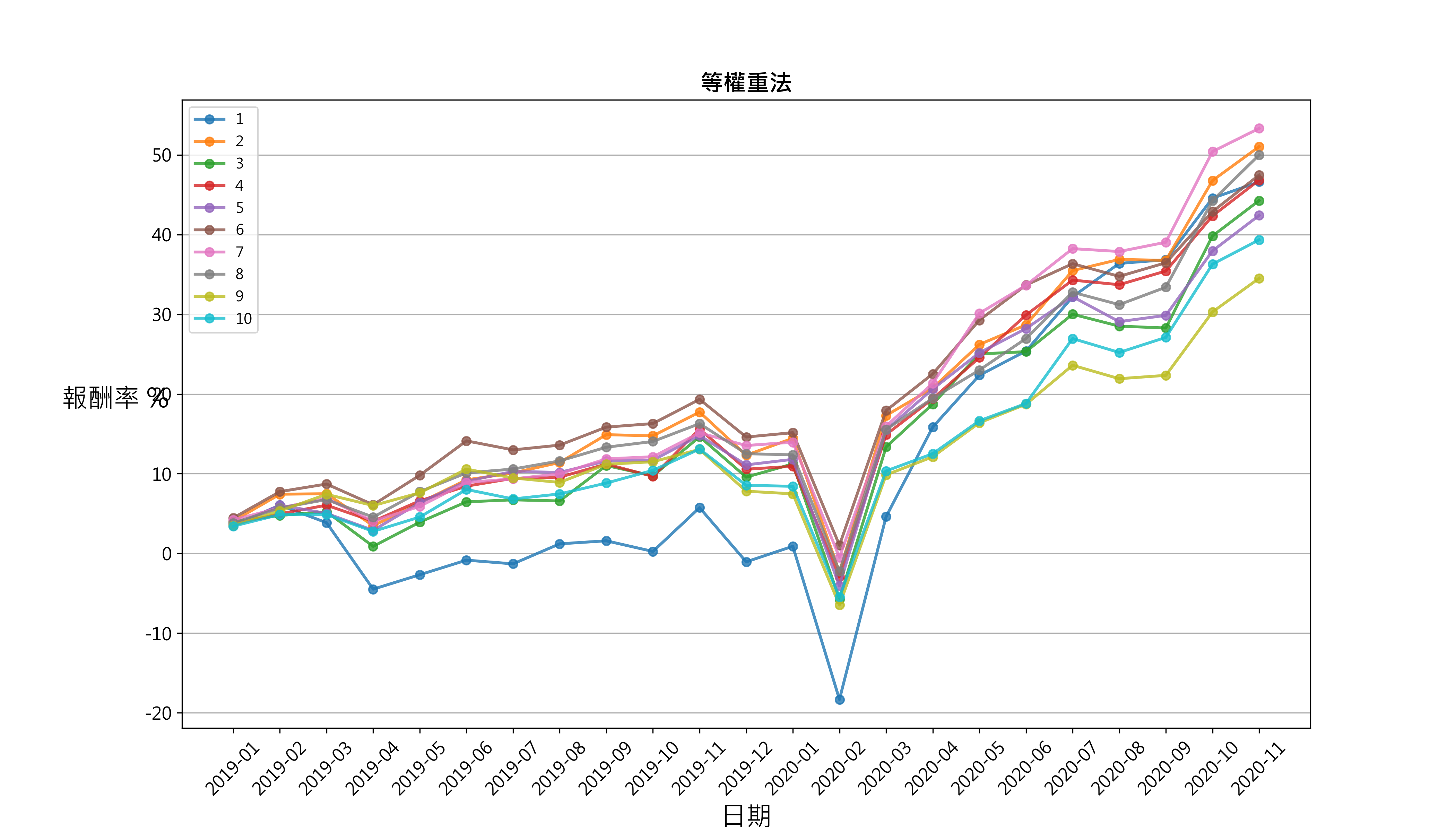
# 比较 等权重法与 IC加权法
data_equal_ir = pd.merge(
pd.DataFrame(data_equal['1']).rename({'1':'等权重法'}, axis=1),
pd.DataFrame(data_ic['1']).rename({'1':'IC加权法'}, axis=1),
how='inner',left_index=True, right_index=True)draw_group_return(data_equal_ir, '等权重法 vs IC加权法')

比较两种权重法的第一组，也就是 ROE最大与股价净值比最小的分组。

结论

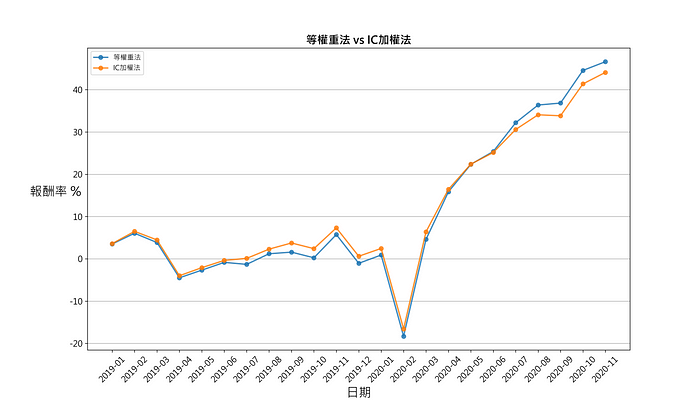
发现 2019年初到 2020年底股价净值比与 ROE合成的因子分组绩效并没有呈现稳定的单调性与区分度，分组的累积绩效线有时甚至会纠结，分析结果可能原因是交易频率过高，ROE只有季资料，合成因子受股价净值比影响较大。再者发现等权重法与 IC加权法在不同时段内，并没有显著差异。

未来可试著降低交易频率，以及回测不同的因子组合，挖掘出有稳定单调性与区别度的因子组合，再进一步优化因子权重。如果读者对于其他因子资料有兴趣，欢迎到 TEJ E-Shop 选择最适的方案，找出具有获利性、稳定性与可解释性的因子！

完整程式码

• 点此前往Github

延伸阅读

• ESG量化因子选股
• 效率前缘曲线

相关连结

• TEJ API 资料库首页
• TEJ E-Shop 完整资料库购买