
目录
现金增资是上市柜公司常见的筹资方式,目的为扩大资本支出、偿还相关债务以及改善财务结构等,但有不少文献指出,这种借钱的举动会向市场发出负面的讯号,公司股价因此时常在宣告现金增资时应声下跌。
而事件研究法即是研究公司重大事件(购并、增资、股票回购…)或是金融市场事件(制度改革、政策、总经…),对于公司价值影响的一种统计方法。一般而言,主要依循以下步骤进行 : 事件日确定、定义估计期间与事件发生期间、计算异常报酬率、统计检验。因此本周我们透过 TEJ API的资料库,来观察现金增资宣告是否真的会对台湾上市公司价值造成影响吧!
本文使用 Windows OS 并以 Jupyter Notebook 作为编辑器
import tejapi import pandas as pd import numpy as np import matplotlib.pyplot as plt from sklearn.linear_model import LinearRegression from scipy import stats tejapi.ApiConfig.api_key = 'Your Key' tejapi.ApiConfig.ignoretz = True
Note: sklearn.linear_model用于回归分析;scipy用于统计检定
tse_stocks 列表security = tejapi.get('TWN/ANPRCSTD',
mkt = 'TSE',
stypenm = '普通股',
opts = {'columns':['coid','mdate','stypenm','mkt']},
paginate = True,
chinese_column_name = True)
tse_stocks = security['证券码'].tolist()
events = tejapi.get('TWN/ASTK1',
x_mt_date = {'gte':'2019-01-01', 'lte':'2021-08-01'},
opts = {'columns':['coid','cash','x_mt_date']},
paginate = True,
chinese_column_name = True)
本文以股东会决议日为事件发生日,并选取 2019~2021年8月之间的事件
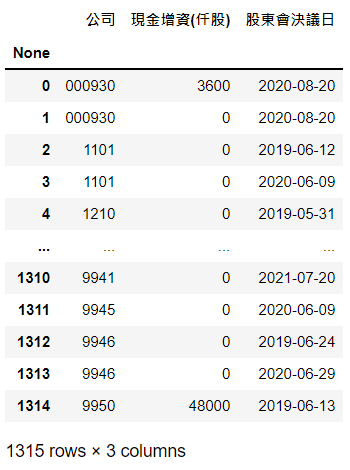
cash = events[events['现金增资(仟股)']>0].reset_index(drop=True)
除了现金增资外,亦包含盈余、公积增资等事件,而本文以现金增资为主
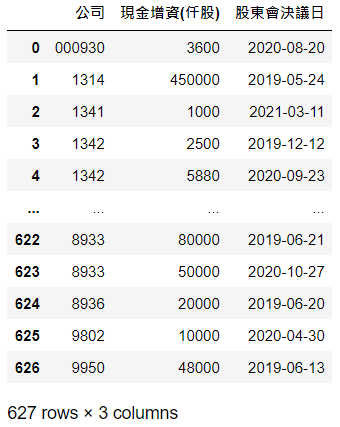
tse_cash = cash[cash['公司'].isin(tse_stocks)].reset_index(drop=True)
利用上市公司代码tse_stocks 与 isin(),筛选出 cash表格有涵盖上市公司代码的资料
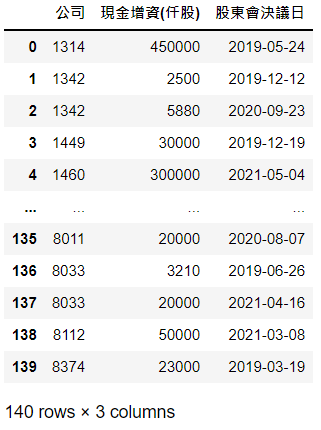
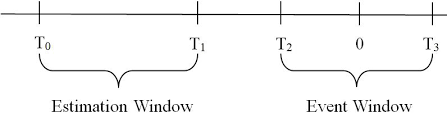
估计期间 (T0 ~ T1):设 -260期 ~ -10期,此期间的报酬与 Fama & French 5因子投组报酬跑回归,得到公司各因子的估计系数,其将用于计算事件期间的预期报酬
事件日 (0): 股东会决议日,因其为市场接收到现金增资事件的最早时点
事件期间 (T2 ~ T3):设 -5期 ~ +5期,计算此期间实际报酬与 Fama & French 模型所预测出的报酬差异,得到异常报酬
因涵盖 140 起现金增资宣告事件,故以回圈的方式进行每个事件的运算,并储存最后结果至 final 变数,而过程中会排除报酬率资料缺漏、初次上市事件。以下撷取回圈部分程式码的重点内容加以解释,并图示第一笔资料 ( stock = ‘1314’, date = ‘2019–05–24’ ) 处理情况帮助理解每个回圈的运作。其余资料处理部分则详见文章下方的完整程式码
return_set = tejapi.get('TWN/APRCD',
coid = stock,
mdate = {'gte': date + pd.Timedelta(days =
-450), 'lte': date + pd.Timedelta(days = 25)},
opts = {'columns' : ['coid', 'mdate','roi']},
paginate = True,
chinese_column_name = True)
利用每起事件的公司 stock、日期 date,捞取事件日前后的报酬率,这边取 -450 ~ 25 天是为了确保拥有完整估计期间 (251交易日)、事件期间 (11交易日)的报酬率
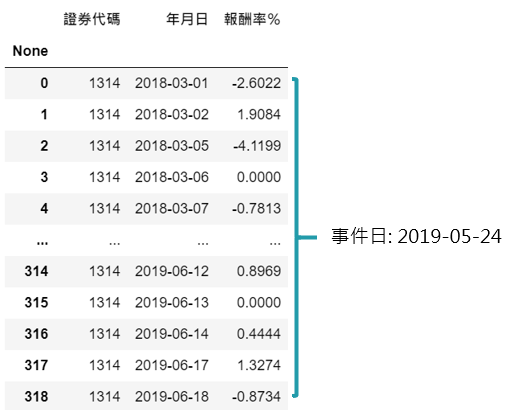
event_index = return_set[return_set['年月日'] == date].index.values.astype(int)[0]
首先找出事件日的索引值,转成数字后储存到 event_index ,以此为基准切割成估计期间、事件期间报酬
estimate_window = return_set[event_index - 260 - 1: event_index - 10].reset_index(drop=True) event_window = return_set[event_index - 5: event_index + 5 + 1].reset_index(drop=True)
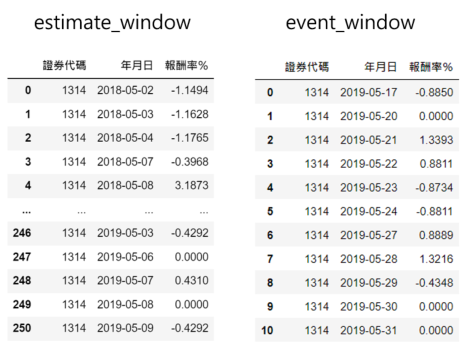
#估计起始日期(-260) estimate_start = estimate_window.loc[0, '年月日'] #事件结束日期(+5) event_end = event_window.loc[5*2, '年月日']
分别找出估计期间的起始日期、事件期间的结束日期,并储存到对应变数。再以此为根据,直接捞出 – 260期 ~ 5期,这段期间的每日市场风险溢酬、规模溢酬、净值市价比溢酬、盈利能力因子、投资因子投组报酬资料,Y9999代表以所有上市公司、简单报酬率计算以上因子投组报酬
fama_french = tejapi.get('TWN/AFACTO1D',
coid = 'Y9999',
mdate = {'gte':estimate_start, 'lte': event_end},
opts = {'columns': ['coid',
'mdate','mrp','smbn','bp','op','inv']},
paginate = True,
chinese_column_name = True)
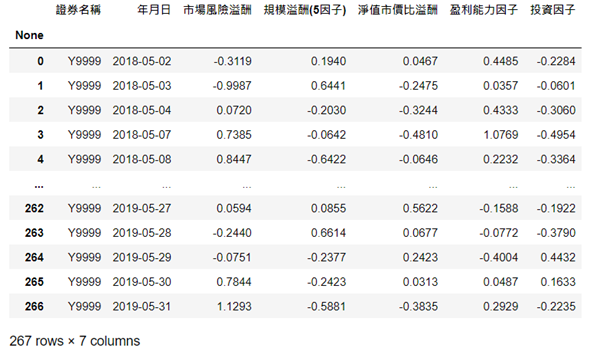
ols_data = estimate_window.merge(fama_french, on = '年月日') x = ols_data.loc[:,['市场风险溢酬', '规模溢酬(5因子)','净值市价比溢酬','盈利能力因子','投资因子']].values y = ols_data['报酬率%'].values.reshape(-1,1) model = LinearRegression() model.fit(x,y)
将估计期间报酬率与 Fame-French 因子报酬合并,并形成带入回归模型所需的二维阵列应变数(公司报酬率) 与自变数 (因子报酬),最后再带入模型
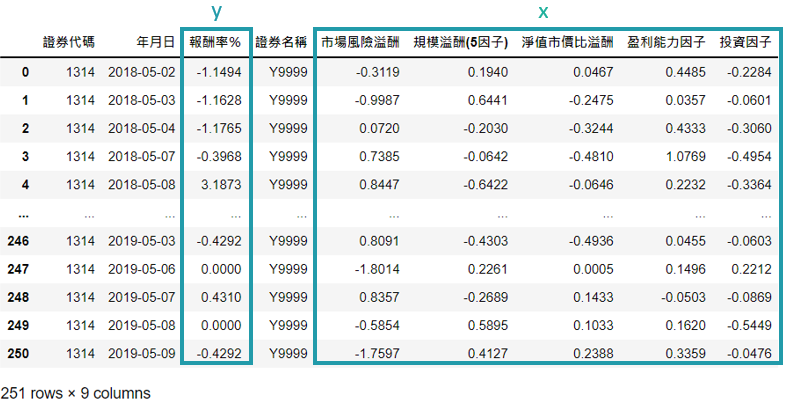
predict_data = event_window.merge(fama_french, on = '年月日') event_x = predict_data.loc[:,['市场风险溢酬','规模溢酬(5因子)','净值市价比溢酬','盈利能力因子','投资因子']].values
将事件期间报酬率与 Fame & French 因子报酬合并,并将这段期间的因子投组报酬储存,其将用于计算预期报酬的自变数,因此将其置入已有估计系数的模型 model.predict()算出预期报酬,接著即可算出异常报酬率、累计异常报酬率。这边最后加上相对天数栏位,将用于最后所有事件的分群计算。
event_window['预期报酬率'] = model.predict(event_x) event_window['异常报酬率'] = event_window['报酬率%'] - event_window['预期报酬率'] event_window['累计异常报酬率'] = event_window['异常报酬率'].cumsum() event_window['相对天数'] = [i for i in range(-5, 5 + 1)]
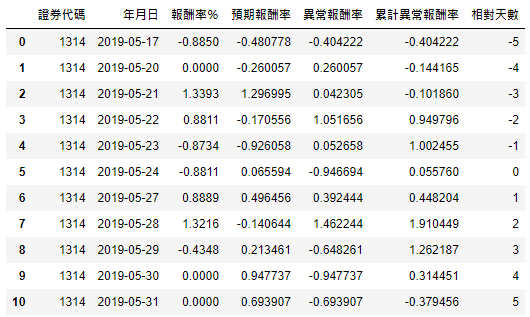
每个事件 (回圈) 重复以上基本步骤,并将最后将结果都附加在 final 表格,以下为 final 最终结果
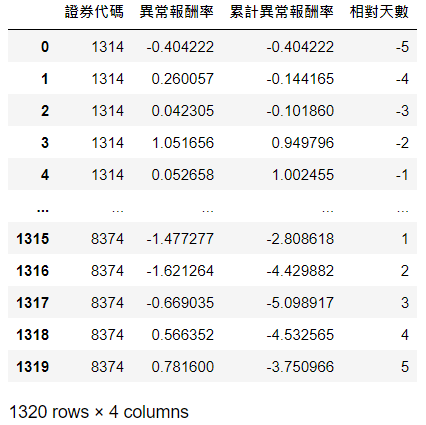
sorted_data = final.groupby(by = '相对天数').mean().reset_index()
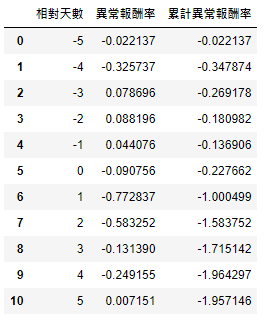
plt.plot(sorted_data['相对天数'], sorted_data['异常报酬率'], label = 'Average Abnormal Retrun')
plt.plot(sorted_data['相对天数'], sorted_data['累计异常报酬率'], label = 'Cumulative Abnormal Return')
plt.xlabel('Event Day')
plt.title('Event Study')
plt.xticks(np.arange(-5, 5+1 , 1))
plt.legend()
plt.show()
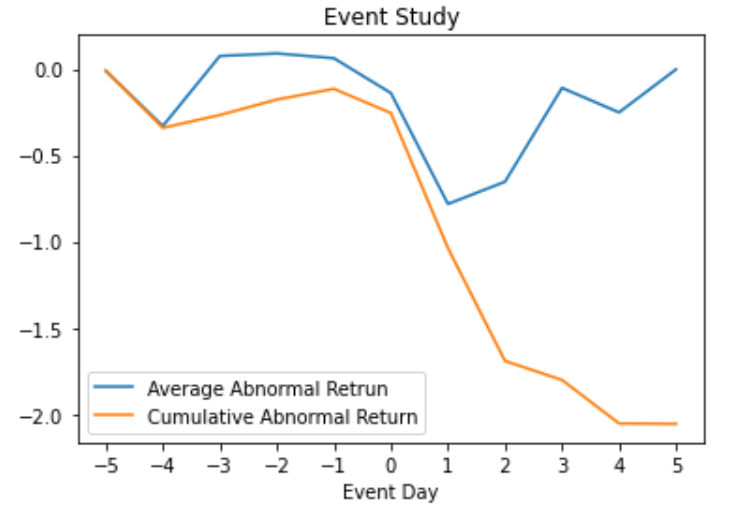
可以看到,在宣告现金增资日后的几天,出现明显地异常负报酬,但到了第三天后,异常报酬恢复到 0 左右,可能代表市场已经消化这个资讯
ttest = pd.DataFrame()
for day in range(-5,5+1):
sample = final[final['相对天数'] == day]['异常报酬率'].values
t, p_value = stats.ttest_1samp(sample, 0)
if p_value <= 0.01:
significance = '***'
elif 0.01 < p_value <= 0.05:
significance = '**'
elif 0.05 < p_value <= 0.1:
significance = '*'
else:
significance = ''
ttest = ttest.append(pd.DataFrame(np.array([day,t,p_value, significance]).reshape((1,4)), columns = ['相对天数','T检定值', 'P-value','显著水准'],)).reset_index(drop=True)
ttest = ttest.set_index('相对天数')
利用 stats.ttest_lsamp() 进行T检定,检验每个相对日的异常报酬是否显著异于 0。最后再根据 P 值自行加上显著性星星,最后整理成 ttest 表格
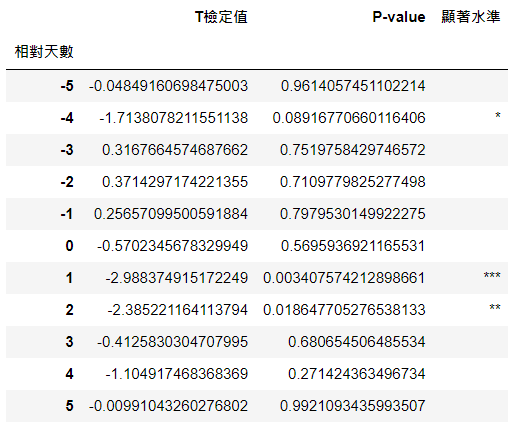
此时可以推论,在现金增资宣告日的后1、2日,公司的价值显著受到影响,推测是因为公司通常于盘后宣告重大决议,因此股价于次日交易日开始反应
经过这一连串的操作,相信读者对于事件研究有了进一步的认识!过程中有许多假设可以自行调整、或是参考对应领域的文献,例如估计期间、事件期间与异常报酬的计算方式,而这当中运用到的资料,都能从 TEJ API 资料库快速捞取下来,直接省略事前资料爬取、清理、计算等繁琐步骤。若读者有兴趣验证其他经济事件对公司的影响,推荐到 TEJ E Shop,选购最符合自身需求的方案!

电子报订阅