基金相似度比较

May 23 2023

本文重点概要

文章难度：★★★☆☆
使用基金基本资料进行相似度分析
阅读建议：本文主要将欧式距离、余弦相似度等公式程式化，公式的推导并不在这次文章的范畴内，建议读者再阅读前，先了解欧式距离、余弦相似度的原理。

前言

投资一定会伴随著风险，然而并不是所有风险都是无可必免的，每个人心里都不免会有「损失厌恶」的情节产生，透过分散投资，将资金分散在不同的市场之中，由于资产类别的不同，投资人可以有效管理风险，并减低市场波动对投资组合的影响，本篇文章将主要探讨如何使用数据，以客观科学的角度比较基金之间的相似程度。

编辑环境与模组需求

本文使用 MacOS 作业系统以及 Jupyter Notebook 作为编辑器

# 载入所需套件
import pandas as pd 
import re
import numpy as np 
import tejapi
import plotly.graph_objects as go
import random
import seaborn as sns
import math

# 登入TEJ API
api_key = 'YOUR_KEY'
tejapi.ApiConfig.api_key = api_key
tejapi.ApiConfig.ignoretz = True

资料库使用

基金基本资料(TWN/AATT)

资料导入

fund = tejapi.get('TWN/AATT',
                   paginate = True,
                   opts = {
                       'columns':['coid', 'mdate', 'isin',
                                  'fld006_c', 'fld007_c', 
                                  'fld014_c','fld015',
                                  'fld016_c','un_name_c',
                                  'risk', 'main_flag', 
                                  'fld021', 'currency', 'aunit1',
                                 ]
                   }
                  )

资料处理

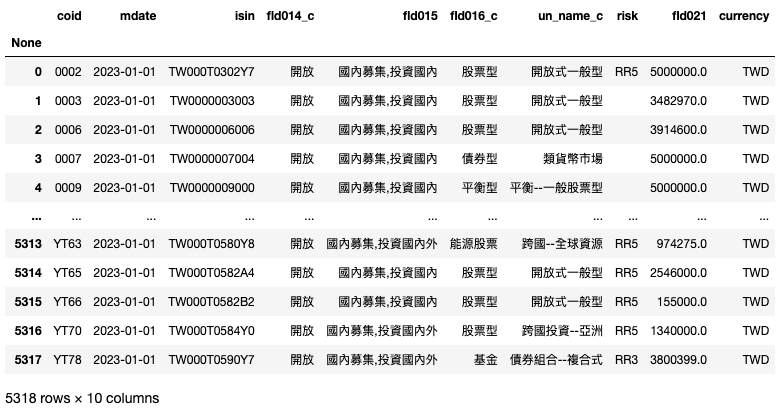
本次实作所需要的栏位有:

isin : 基金ISIN Code
fld014_c : 类型(开放型基金/封闭型基金)
fld015 : 型态(目前就基金资金募集地及投资区域)
fld016_c : 投资标的
risk : 风险收益等级
fld021 : 成立资产(千元)
currency : 币别

由于大多数栏位为文字资料，因此在资料预处理时要先将其转换为序数，一般这样的做法可以直写使用ordinal encoding的相关套件，但由于投资标的的类型间存在著风险大小的关系，因此本次实作就自行定义各类别的相应序数，以确保之间的相对风险关系正确。

为了给予序数，我们将资料表内投资标的的所有类别打印出来

fund["fld016_c"].unique()

style = {
    '':0,
    '保本型': 1,
    '货币型': 2,
    '债券型': 3,
    '平衡型': 4,
    'ETF': 5,
    '指数型基金': 6,
    '基金': 7,
    '多重资产': 8,
    '股票型': 9,
    '房地产': 10,
    '产证券化': 11,
    '不动产证券化': 12,
    '科技股': 13,
    '小型股资': 14,
    '能源股票': 15,
    '期货商品': 16,
}

risk = {
    "":0,
    "RR1":1,
    "RR2":2,
    "RR3":3,
    "RR4":4,
    "RR5":5,
}

area = {
    "国内募集,投资国内":1,
    "国内募集,投资国内外":2,
    "国外募集,投资国内":3,   
}

OorC = {
    "封闭":0,
    "开放":1,
}

# adjust sting data to Ordinal encoding data
fund_adj = fund.copy()
fund_adj["fld015"] = fund_adj["fld015"].apply(lambda x: area.get(x))
fund_adj["fld016_c"] = fund_adj["fld016_c"].apply(lambda x: style.get(x))
fund_adj["risk"] = fund_adj["risk"].apply(lambda x: risk.get(x))
fund_adj["fld014_c"] = fund_adj["fld014_c"].apply(lambda x: OorC.get(x))

再来由于需要使用视觉化图表呈现基金的相似程度，各数值间需要进行尺度的缩放以符合图表规格，因此这里我们对于「成立资产」进行正规化，将数字范围更改为介于 0 ~ 17 之间( 因为投资标的的最大序数为16 )，经过此处理后「成立资产」仅能呈现不同基金成立金额间的比例差距，不再具有真实的金额意义。

# min-max normalization
size = np.array(fund_adj["fld021"].fillna(0))
size = (size - size.min()) / (size.max() - size.min())*len(style)
fund_adj["fld021"] = size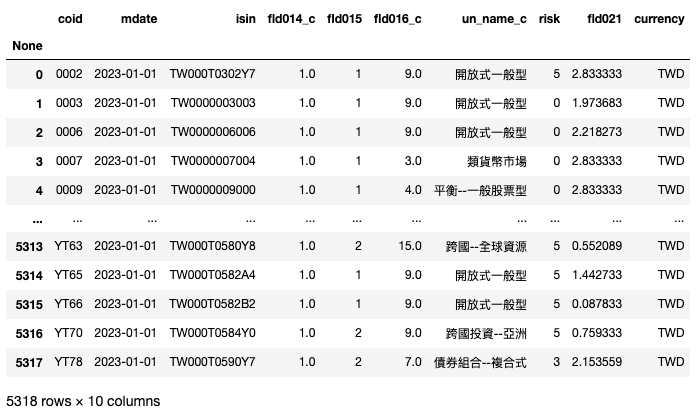

雷达图视觉化

我们筛选币别为新台币的基金进行视觉化图表呈现，本次将以雷达图呈现基金之间的差异程度，我们随机在资料集中抽取 10 档基金来进行相似度比较。

fund = fund[fund["currency"].str.contains("TWD")]

# randomly pick 10 funds
# set the random state
isin_lst = list(fund["isin"].unique())

random.seed(1)
random_isin_lst = random.sample(isin_lst, 10, )

check_lst = random_isin_lst
categories = ['开放型基金/封闭型基金','募集地及投资区域','投资标的',
              '风险', '成立资产']

fig = go.Figure()
data_lst = []
for num, isin in enumerate(check_lst):
    
    data = list(fund_adj[fund_adj["isin"] == isin][["fld014_c", "fld015", "fld016_c", "risk", "fld021"]].iloc[0, :])
    data_lst.append(data)
    
    fig.add_trace(go.Scatterpolar(
          r=data,
          theta=categories,
          fill='toself',
          name=isin
    ))
    
    
fig.update_layout(
  polar=dict(
    radialaxis=dict(
      visible=True,
      range=[0, len(style)]
    )),
  showlegend=True
)

fig.show()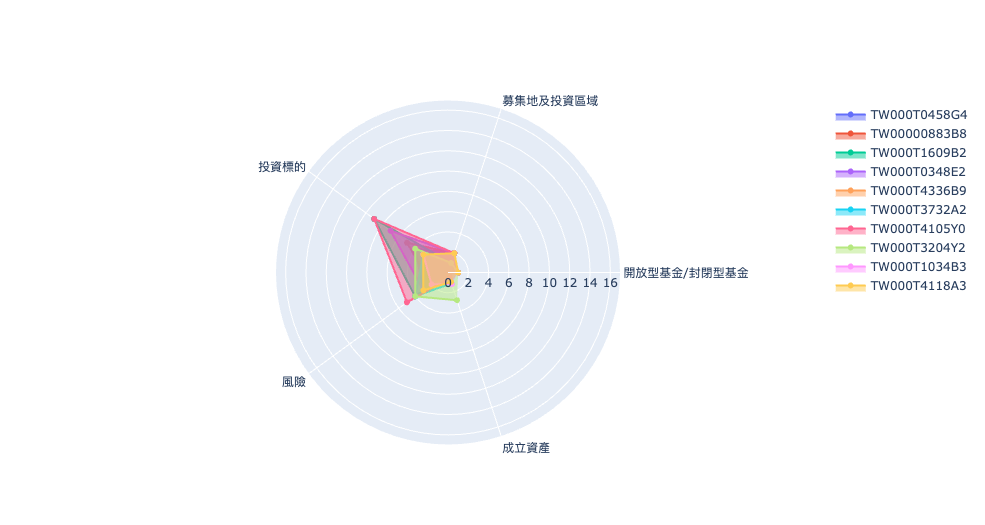

雷达图可以清晰快速的帮助我们了解各基金项目之间差别，然而它却无法给予我们一个具体的数值关于到底两档基金之间有多相似，因此接下来将使用余弦相似度 与 欧式距离 来解决上述问题。

欧式距离

全称为欧几里德距离 (Euclidean distance)，是一种常见的距离度量方法，用于计算多维空间中任意两点的直线距离，接下来我们透过程式建立出欧式距离的相关矩阵。

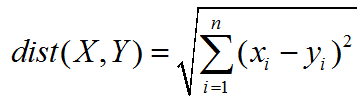
# calculate Euclidean Distance of each couple funds
ED_matrix = np.empty(shape=[len(random_isin_lst), len(random_isin_lst)])
for i in range(len(data_lst)):
    for j in range(len(data_lst)):
        dist = math.dist(data_lst[i], data_lst[j])
        ED_matrix[i, j] = round(dist,5)
print(ED_matrix)
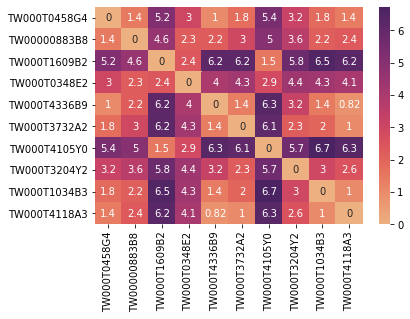
sns.heatmap(ED_matrix, xticklabels = random_isin_lst, yticklabels = random_isin_lst, annot=True, cmap = "flare")

如此，我们已经完成欧式距离的计算，但其以矩阵形式呈现的结果非常不好判读，因此我们再使用另一种视觉化图表-热力图来显示结果

在欧式距离之中，在未将数据标准化或正规化的情况下，数值并没有上限，0 代表完全相同，而数值越大代表著两元素间的距离越远，也就是差异越大。而在热力图中，横轴与纵轴为基金的ISIN code ，而左上至右下的斜对角代表对应到的元素皆为自己，因此距离永远为 0 。

余弦相似度

余弦相似度 (Cosine Similarity)通过测量两个向量的夹角的余弦值来衡量之间的相似性。 0 度角的余弦值是 1，代表完全相同，而其他任何角度的余弦值都不大于 1；并且其最小值是 -1。从而两个向量之间的角度的余弦值确定两个向量是否大致指向相同的方向。

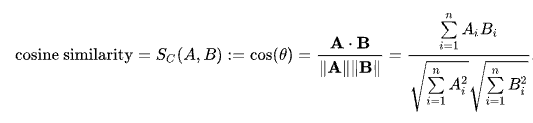
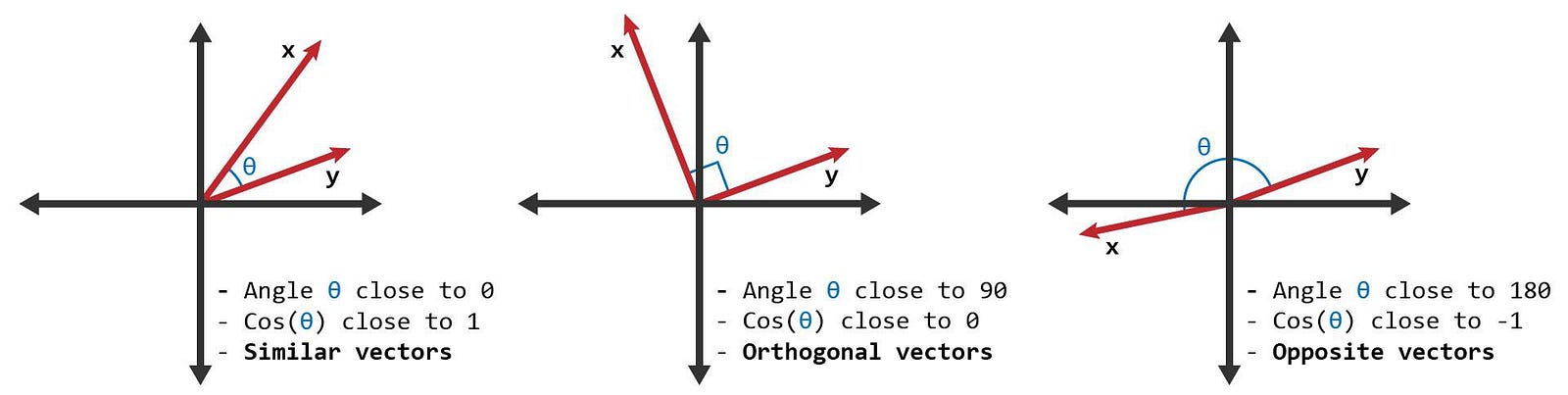
接著我们将公式程式化，作法与计算欧式距离类似，值得注意的是，余弦相似度不会因为向量的大小而有差异，这是由于余弦相似度的计算过程中恰好做了类似正规化的处理。

# The measure of cosine similarity will not be affected by the size of the vector
CS_matrix = np.empty(shape=[len(random_isin_lst), len(random_isin_lst)])
for i in range(len(data_lst)):
    for j in range(len(data_lst)):
        A = np.array(data_lst[i])
        B = np.array(data_lst[j])
        cosine = np.dot(A,B)/(norm(A)*norm(B))
        CS_matrix[i, j] = round(cosine,5)
print(CS_matrix)  
sns.heatmap(CS_matrix, xticklabels = random_isin_lst, yticklabels = random_isin_lst, annot=True, cmap = "flare_r")

查看余弦相似度相关矩阵

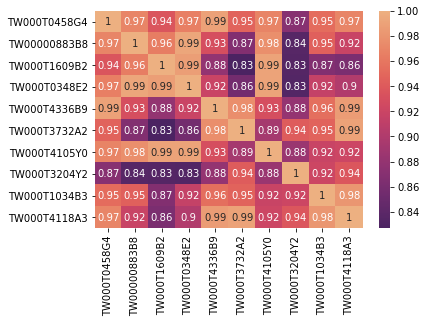
此时眼尖的朋友应该有注意到，欧式距离是数值越小越相似，而余弦相似度则是数值越大越相似，两者呈现反关系，因此在热力图呈现时应该要讲图表颜色倒转才比较方便比较两种计算结果，因此在欧式距离视觉化程式码中的 cmap = “flare” 在这里要改为 cmap = “flare_r”。

比较两张图，大致上的分布趋势都相应符合，因为事实上欧式距离就等价于余弦相似度。

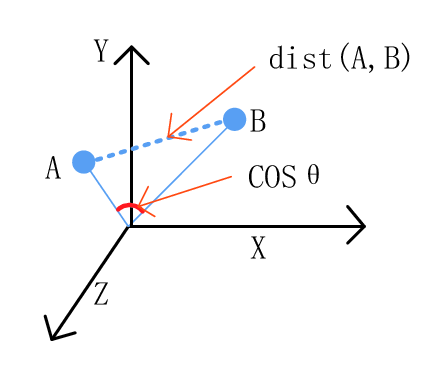
先假设空间中有两点：A、B
针对 A、B 分别做正规化，所得到的结果即为单位向量
以两单位向量计算余弦相似度，其分母为 1 所以在此就直接省略
再以两单位向量计算其欧式距离，经化简后即可得证

那这样的话，欧式距离与余弦相似度的差别到底是什么呢？
对于欧式距离来说，由于它计算的是两点之间的直线距离，因此当两点的趋势相同，但向量长度不同时，欧式距离就无法反映出这样的相似性；以本次实作来举例，当两档基金的相似程度极大，只是其中一档的成立资产较大、另一篇较小时，虽然两档基金性质相似，但由于成立资产大小的问题，欧式距离的计算结果仍然会是差距很远。另一方面，余弦相似度是计算两向量的余弦夹角，因此相似的两档基金夹角会很小，因此就可以有效显示出它们之间的相似性。

结语

在相似度的比较结果上我们可以发现几乎大多数的境内基金之间相似程度都非常高，这非常有可能是由于本次实作仅仅筛选了基金基本资料的一些资讯，因此仅能反映当初基金成立时的状态，读者可以在自行加入其他资讯进行计算，例如报酬率、费用率等等，TEJ API 提供完整的基金资讯以及多种取用方式可让读者随心所欲，客制化自己的比较模组。

温馨提醒，本次介绍与标的仅供参考，不代表任何商品或投资上的建议。之后也会介绍使用TEJ资料库来建构各式选择权模型，所以欢迎对选择权交易有兴趣的读者，选购TEJ E-Shop的相关方案，用高品质的资料库，建构出适合自己的订价模型。

完整程式码

点此前往Github