寻找Alpha

Jan 09 2023

透过Fama&French三因子模型所得到的alpha，来建构long-short strategy，并回测与大盘的绩效比较。

本文重点概要

文章难度：★★☆☆☆

使用Fama&French三因子模型来计算台湾上市柜股票的alpha，并取得alpha最高的前20%股票以及alpha最低的20%股票，做一个多空策略的投资组合，并评断绩效。

阅读建议：本文会从三因子模型的建立开始，计算出SMB以及HML，因此需要对投资学里的资本资产定价模型(CAPM)有初步认识，并且了解alpha以及beta的概念，对阅读文章会更有帮助。

前言

资本资产定价模型(CAPM)，在现代投资组合理论中占据了相当重要的地位，也是现代金融市场价格理论的基础，而后续许多学者不断在此基础上延伸，开创了各式各样的因子模型，甚至有因子动物园(factor zoo)之说，如本文使用的Fama&French的三因子模型，是将原本CAPM仅考虑市场风险因子的部分，而外加入了规模溢酬以及B/M ratio溢酬，以期待投资组合或股票的报酬率，能被这三个因子所解释。

编辑环境及模组需求

本文使用Mac OS并以jupyter作为编辑器

import pandas as pd
import numpy as np
import tejapi
import statsmodels.api as sm
import matplotlib.pyplot as plt
import matplotlib.transforms as transforms
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS'] # 解决MAC电脑 plot中文问题
plt.rcParams['axes.unicode_minus'] = False
tejapi.ApiConfig.api_key ="Your Key"
tejapi.ApiConfig.ignoretz = True

资料库使用

调整股价(日)-除权息调整(TWN/APRCD1)
证券属性资料(TWN/ANPRCSTD)

资料导入

资料期间取自2014年到2021年6月，分别取得了上市柜股票代码、收盘价、报酬率、市值以及股价净值比资料。

data=tejapi.get('TWN/ANPRCSTD' ,chinese_column_name=True )
select=data["上市别"].unique()
select=select[1:3]
condition =(data["上市别"].isin(select)) & ( data["证券种类名称"]=="普通股" )
data=data[condition]
twid=data["证券码"].to_list()  #取得上市柜股票证券码

df = pd.DataFrame()
for i in twid: #资料笔数超过100万笔，透过回圈方式抓取
    df = pd.concat([df, tejapi.get('TWN/APRCD1',  #从TEJ api捞取所需要的资料
                  chinese_column_name = True,
                  paginate = True,
                  mdate = {'gt':'2013-12-31', 'lt':'2022-07-01'},
                  coid=i,
                  opts={'columns':['coid','mdate', 'close_adj' ,'roi' ,'mv', "pbr_tej"]})])

先将股价净值比取倒数得到帐面市值比，再取得每日市值的中位数，并将大于中位数的股票标记为B，小于中位数的标记为S，形成两个投资组合。

df['帐面市值比'] = 1/df['股价净值比-TEJ']

ME = df.groupby('年月日')['市值(百万元)'].apply(lambda x: x.median())
ME.name = '市值_中位数'
df = df.merge(ME, on='年月日')
df['市值matrix'] = np.where(df['市值(百万元)']>df['市值_中位数'], 'B', 'S')

将大型股投资组合与小型股投资组合，用市值加权的方式，得到投资组合的权重，并确认两个投资组合的权重总合是否都等于1。

df1 = (df.groupby(['年月日','市值matrix'])['市值(百万元)'].sum()).reset_index()
df = df.merge(df1, on=['年月日','市值matrix'])
df['weight'] = df['市值(百万元)_x']/df['市值(百万元)_y']
df.groupby(['年月日','市值matrix'])['weight'].sum()

df.groupby(['年月日','市值matrix'])['weight'].sum()

计算投资组合的报酬率，并将小型股投组报酬率减掉大型股投组报酬率，组合成一个long-short portfolio，完成SMB因子。

df['return1'] = df['报酬率％']* df['weight']
SMB = df.groupby(['年月日','市值matrix'])['return1'].sum()
SMB.reset_index(inplace=True)
SMB.set_index('年月日',drop=True, inplace=True)
SMB = SMB[SMB['市值matrix']=='S']['return1'] - SMB[SMB['市值matrix']=='B']['return1']
SMB.name = 'SMB'
SMB

Fama&French将 BM ratio分成30%, 40%, 30%，因此我取得30百分位数以及70百分位数的BM_ratio，并将大于70百分位数的标记为V(value)，小于30%的标记为G(growth)，其余的则标记为N(Neutral)，形成三个投资组合。

a = df.groupby('年月日')['帐面市值比'].quantile(0.7)
a.name = 'BM_0.7'
b = df.groupby('年月日')['帐面市值比'].quantile(0.3)
b.name = 'BM_0.3'
df = df.merge(a, on='年月日')
df = df.merge(b, on='年月日')
df['BM_matrix'] = np.where(df['帐面市值比']>df['BM_0.7'], 'V', (np.where(df['帐面市值比']<df['BM_0.3'],'G', 'N')))

一样使用市值加权的方式来计算三个投资组合的权重，并确认权重是否总和为一。

df2 = (df.groupby(['年月日','BM_matrix'])['市值(百万元)_x'].sum()).reset_index()
df = df.merge(df2, on=['年月日','BM_matrix'])
df['weight2'] = df['市值(百万元)_x_x']/df['市值(百万元)_x_y']
df.groupby(['年月日','BM_matrix'])['weight2'].sum()

计算投资组合的报酬率，并将价值股投组报酬率减掉成长股投组报酬率，组合成一个long-short portfolio，完成HML因子。

df['return2'] = df['报酬率％']* df['weight2']
HML = df.groupby(['年月日','BM_matrix'])['return2'].sum()
HML.reset_index(inplace=True)
HML.set_index('年月日',drop=True, inplace=True)
HML = HML[HML['BM_matrix']=='V']['return2'] - HML[HML['BM_matrix']=='G']['return2']
HML.name = 'HML'
HML

将计算好的SMB和HML因子合并

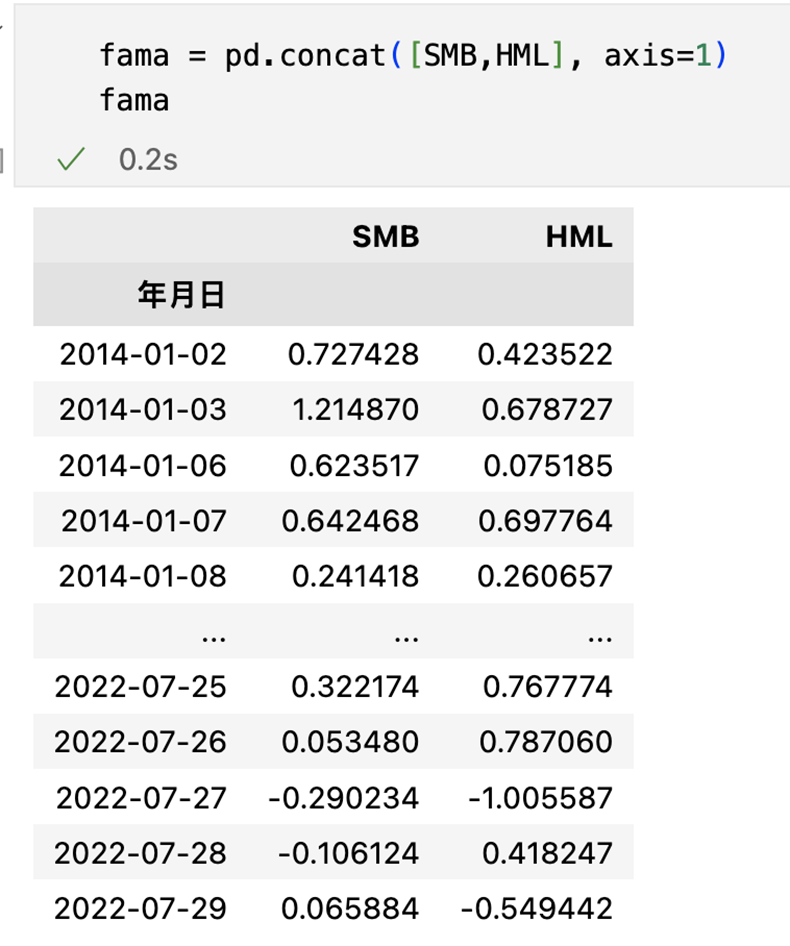
抓取大盘的报酬率，作为三因子模型中第一个的市场因子

Y9999 = tejapi.get('TWN/APRCD1',  #从TEJ api捞取所需要的资料
                  chinese_column_name = True,
                  paginate = True,
                  mdate = {'gt':'2013-12-31', 'lt':'2022-07-01'},
                  coid='Y9999',
                  opts={'columns':['coid','mdate', 'roi']})

把三个因子合并成一张表

fama = fama.merge(Y9999[['年月日','报酬率％']], on='年月日')
fama.rename(columns = {'报酬率％':'rm'}, inplace=True)
fama.set_index('年月日',drop=True,inplace=True)
fama

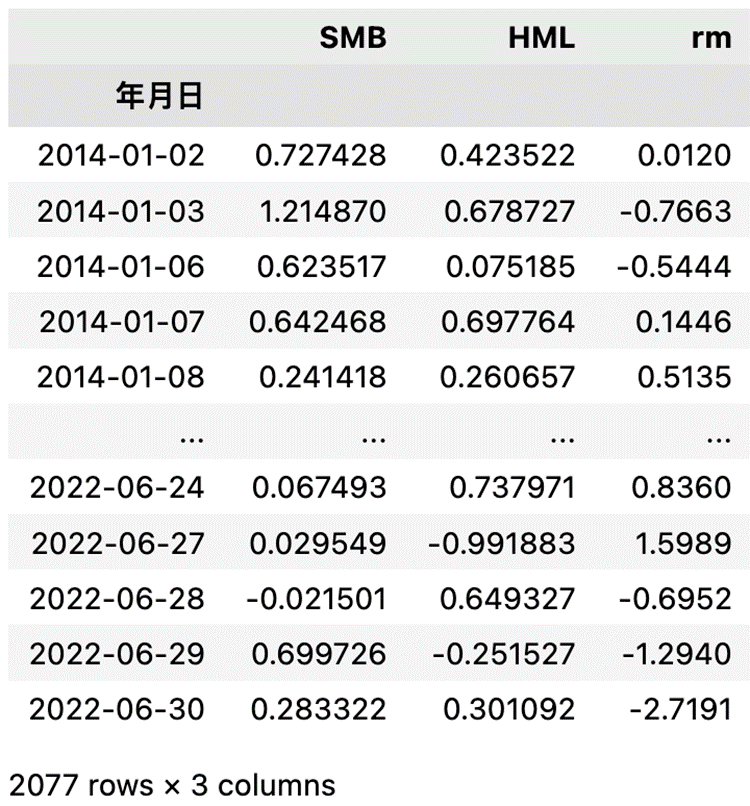
将个股的报酬率筛选出来

stock = df[['证券代码', '年月日','报酬率％']]
stock.set_index('年月日', drop=True, inplace=True)
stock = stock.loc[:'2022-06-30']
stock

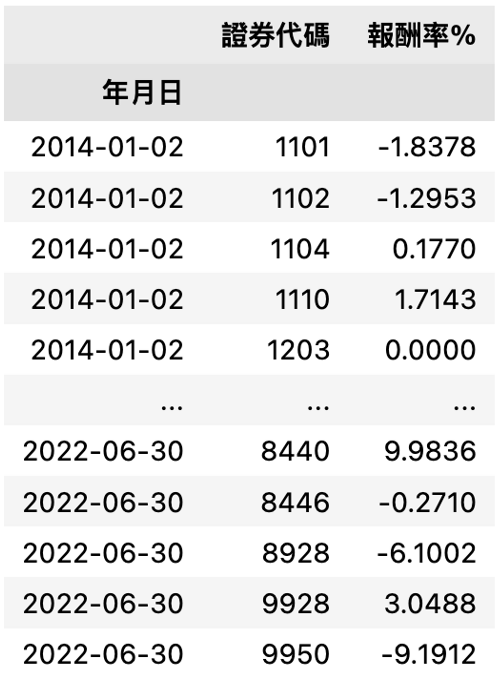
我们目标的投资组合是将所有股票前20%的alpha扣掉后20%的alpha，组合出一个多空策略，权重部分采用等权重法，再平衡的方式为每半年调整一次，将使用前半年资料筛选出的投组，用在下半年并进行回测。

m = pd.date_range('2013-12-31', '2022-07-31', freq='6M').to_list()
X = sm.add_constant(fama)
stock_list = stock['证券代码'].unique()

b = pd.DataFrame()
for j in stock_list:
    a=[]
    for i in range(len(m)-1):
        try:
            Y = (stock[stock['证券代码']== j]).loc[m[i]:m[i+1]]
            result = sm.OLS(Y['报酬率％'], X.loc[m[i]:m[i+1]]).fit()
            a.append(result.params[0])
        except:
            pass
    j = str(j)
    c = pd.DataFrame({'证券代码':([j]*len(a)), 'alpha':a}, index=m[1:len(a)+1])
    b = pd.concat([b,c])
b.index.name = '年月日'

计算出第80百分位数以及第20百分位数的alpha数值，并将大于80百分位数的个股筛选出来形成做多投组，小于20%的形成做空投组。

alpha1 = b.groupby('年月日')['alpha'].apply(lambda x : x.quantile(0.8))
alpha1.name = 'alpha0.8'
alpha2 = b.groupby('年月日')['alpha'].apply(lambda x : x.quantile(0.2))
alpha2.name = 'alpha0.2'
b = b.merge(alpha1, on='年月日')
b = b.merge(alpha2, on='年月日')
long = (b.where(b['alpha'] > b['alpha0.8'])).dropna()
short = (b.where(b['alpha'] < b['alpha0.2'])).dropna()

在计算回测报酬率前先做一些资料预处理

stock1 = df[['证券代码','年月日','收盘价(元)']]
stock1.set_index('年月日',drop=True, inplace=True)
stock1 = stock1.loc[:"2022-06-30"]
stock1['证券代码'] = stock1['证券代码'].astype('str')

计算出做多投组的报酬率以及做空投组的报酬率，并计算此alpha策略的报酬率。

ret = []
for i in range(1, len(m)-1):
    qq = (stock1.loc[m[i]:m[i+1]])['证券代码'].isin((long.loc[m[i]])['证券代码'].tolist())
    a = ((stock1.loc[m[i]:m[i+1]])[qq]).groupby('证券代码')['收盘价(元)'].tail(1).sum()
    b = ((stock1.loc[m[i]:m[i+1]])[qq]).groupby('证券代码')['收盘价(元)'].head(1).sum()
    c = len((long.loc[m[i]])['证券代码'].tolist())
    long_ret = ((a/b)-1)/c
    qq1 = (stock1.loc[m[i]:m[i+1]])['证券代码'].isin((short.loc[m[i]])['证券代码'].tolist())
    a1 = ((stock1.loc[m[i]:m[i+1]])[qq1]).groupby('证券代码')['收盘价(元)'].tail(1).sum()
    b1 = ((stock1.loc[m[i]:m[i+1]])[qq1]).groupby('证券代码')['收盘价(元)'].head(1).sum()
    c1 = len((short.loc[m[i]])['证券代码'].tolist())
    short_ret = ((a1/b1)-1)/c1
    ret.append(long_ret - short_ret)

理论上alpha代表了超额报酬率，也就是可以超过大盘所赚到的报酬率，但从结果发现，利用这个策略形成的投资组合，无论大盘大涨大跌，报酬率皆介于0上下，可见这几个因子已经有失效的疑虑。

y9999  = tejapi.get('TWN/APRCD1',  #从TEJ api捞取所需要的资料
                  chinese_column_name = True,
                  paginate = True,
                  mdate = {'gt':'2013-12-31', 'lt':'2022-07-01'},
                  coid='Y9999',
                  opts={'columns':['coid','mdate', 'close_adj']})

y9999.set_index('年月日' ,drop=True, inplace=True)

a = []
for i in range(1 , len(m)-1):
    b = (((y9999.loc[m[i]:m[i+1]]).tail(1)['收盘价(元)'].values / (y9999.loc[m[i]:m[i+1]]).head(1)['收盘价(元)'].values) -1)[0]
    a.append(b)

ret['大盘'] = a
ret[['ret', '大盘']].apply(lambda x :x*100)

结论

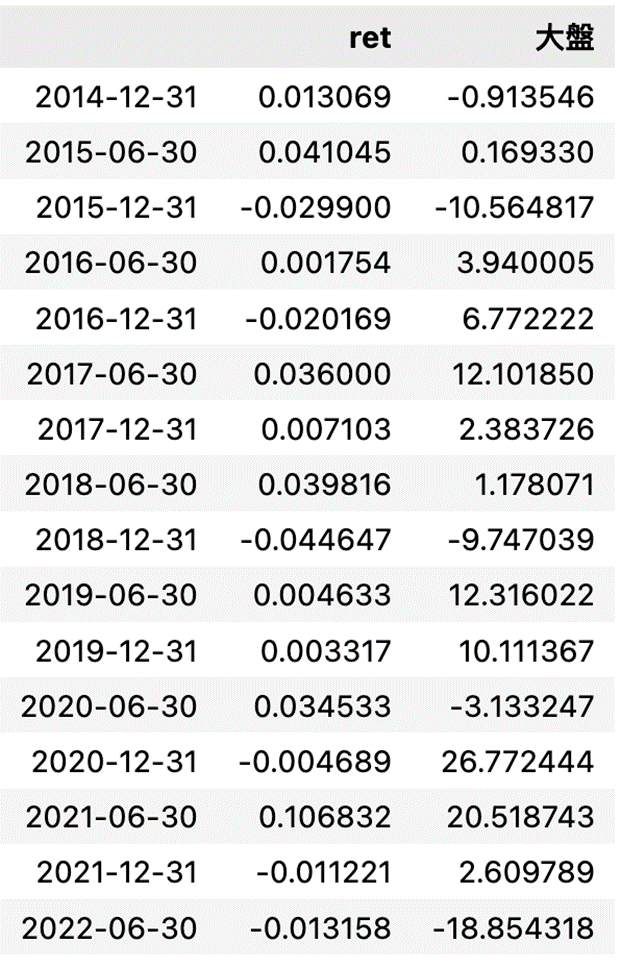
从结果可以看到，我们寻找alpha的投资组合报酬率几乎在0上下，可能原因为Fama&French 的三因子模型发现甚早，存在的异常报酬机会早已被投资人发现，因此失效，读者可以进一步去了解其他因子模型，像是Fama&French 在2015年提出的五因子模型，去实际验证绩效，尽管三因子模型的报酬率看来没有特别好，但仍然是资产定价中非常重要的一部分，在学术与业界中也很多人使用。

之后也会介绍使用TEJ资料库来建构各式指标，并回测指标绩效，所以欢迎对各种交易回测有兴趣的读者，选购TEJ E-Shop的相关方案，用高品质的资料库，建构出适合自己的交易策略。

完整程式码

点此前往Github