选择权定价-蒙地卡罗模拟法

Jul 04 2023

本文重点概要

文章难度：★★★★☆
使用蒙地卡罗模拟定价选择权
介绍变异数缩减方法以增强定价结果

前言

蒙地卡罗模拟法被广泛运用于财务金融领域，股价路径预测中我们已经介绍如何使用蒙地卡罗模拟预测股票价格，今日我们将推广到更难的选择权定价模型。在 CRR模型与 Black-Scholes 模型与 Greeks 两篇文章中，我们分别使用二元树原理与 Black-Scholes 公式解计算买卖权理论价格，其中也解释了许多选择权相关的基础知识，若对选择权一知半解的小伙伴，建议先阅读完这两篇文章后，再回来阅读本篇文章。于之后的章节，我们会先演示如何使用蒙地卡罗法预测股价，再来推广到欧式选择权定价，最后介绍一些变异数缩减方法辅助我们使用蒙地卡罗模拟。

编辑环境与模组需求

本文使用 Window 作业系统以及 Jupyter Notebook 作为编辑器。

# Import required packages
import math
import pandas as pd
import numpy as np 
import matplotlib.pyplot as plt 
import seaborn as sns
from scipy.stats import norm
import time
import tejapi
plt.style.use('bmh')

# Log in TEJ API
api_key = 'YOUR_KEY'
tejapi.ApiConfig.api_key = api_key
tejapi.ApiConfig.ignoretz = True

资料库使用

公司交易面资料库: 未调整股价(日)，资料代码为(TWN/APRCD)。
衍生性金融商品资料库: 选择权日交易状况，资料代码为(TWN/AOPTION)。

资料导入

使用台湾加权股价指数(Y9999)未调整收盘价，时间区间为2021/01/31到2023/04/19。并且载入台湾加权指数买权与卖权(TXO202304C15500、TXO202304P15500)，该选择权为欧式买卖权、开始交易日为1/31，到期日为4/19，履约价格为15500，并且将 “mdate” (日期)栏位设定成索引。

# Import required data
gte, lte = '2021-03-16', '2023-04-20'
stocks = tejapi.get('TWN/APRCD', # stock price
                   paginate = True,
                   coid = 'Y9999',
                   mdate = {'gte':gte, 'lte':lte},
                   opts = {
                       'columns':[ 'mdate','close_d']
                   }
                  )
# Get options price
puts = tejapi.get( # puts price
    'TWN/AOPTION',
    paginate = True,
    coid = 'TXO202304P15500',
    mdate = {'gte':gte, 'lte':lte},
    opts = {
        'columns':['mdate', 'coid','settle', 'kk', 'theoremp', 'acls', 'ex_price', 'td1y', 'avolt', 'rtime']
    }
)
calls = tejapi.get( # calls price
    'TWN/AOPTION',
    paginate = True,
    coid = 'TXO202304C15500',
    mdate = {'gte':gte, 'lte':lte},
    opts = {
        'columns':['mdate', 'coid','settle', 'kk', 'theoremp', 'acls', 'ex_price', 'td1y', 'avolt', 'rtime']
    }
)

资料处理

计算大盘之日报酬并且计算移动报酬波动度，以252天也就是一年为窗格迭代下去。

# Calculate daily return  
stocks['daily return'] = np.log(stocks['close_d']) - np.log(stocks['close_d'].shift(1))
stocks['moving volatility'] = stocks['daily return'].rolling(252).std()

股价预测

我们使用蒙地卡罗模拟股价路径。蒙地卡罗模拟法概念十分简单，就是先取得资产的报酬过程并且将其离散化后，以极小时间区段分区推算资产价格变化。例如以股票价格为例，其报酬服从几何布朗运动，因此可以得到其离散化随机微分过程(式一)，其中的 Wt 为维纳过程。再经过伊藤公式后，就可以得到式二作为蒙地卡罗模拟法的主要方程式进行股价预测，其中的 Zt 为标准常态分配。

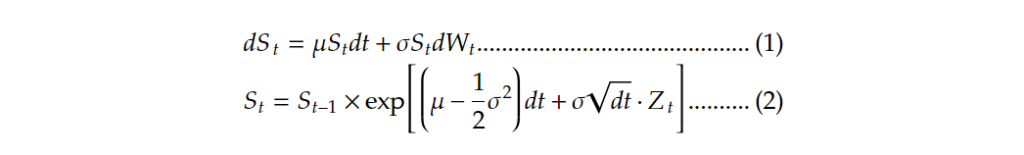
再来我们可以使用 Python 将上式程式化，蒙地卡罗法精髓在于我们同时以式 2 估计多个股价路径，最后将每个路径的最后一个股价加总平均，就会得到是我们欲预测之股价。这里以我们定义以下变数:

S0: 初始日之资产价格。
r: 资产历史报酬率。
sigma: 资产历史报酬波动度。
T: 到期时间。
Nsteps: 切分时间点数量。
Nrep: 股价路径数量。

并且写成 “mc_asset” 函式以执行蒙地卡罗模拟，程式码如下所式。

def mc_asset(S0, r, sigma, T, Nsteps, Nrep):
    SPATH = np.zeros((Nrep, 1 + Nsteps))
    SPATH[:, 0] = S0
    dt = T / Nsteps
    nudt = (r - 0.5 * sigma **2) * dt
    sidt = sigma * np.sqrt(dt)
    
    for i in range(0,Nrep):
        for j in range(0,Nsteps):
            SPATH[i,j+1] = SPATH[i,j] * np.exp(nudt + sidt * np.random.normal())
    return SPATH

完成函式编辑后，我们带入数字检验，并且绘制结果成图 1，图 1 每条线就是一个股价过程。

S0 = 100
K = 110
CallOrPut = 'call'
r = 0.03
sigma = 0.25
T = 0.5
Nsteps = 10000
Nrep = 1000
SPATH = mc_asset(S0, r, sigma, T, Nsteps, Nrep)

plt.figure(figsize = (10,8))
for i in range(len(SPATH)):
    plt.plot(SPATH[i])
plt.xlabel('Numbers of steps')
plt.ylabel('Stock price')
plt.title('Monte Carlo Simulation for Stock Price')
plt.show()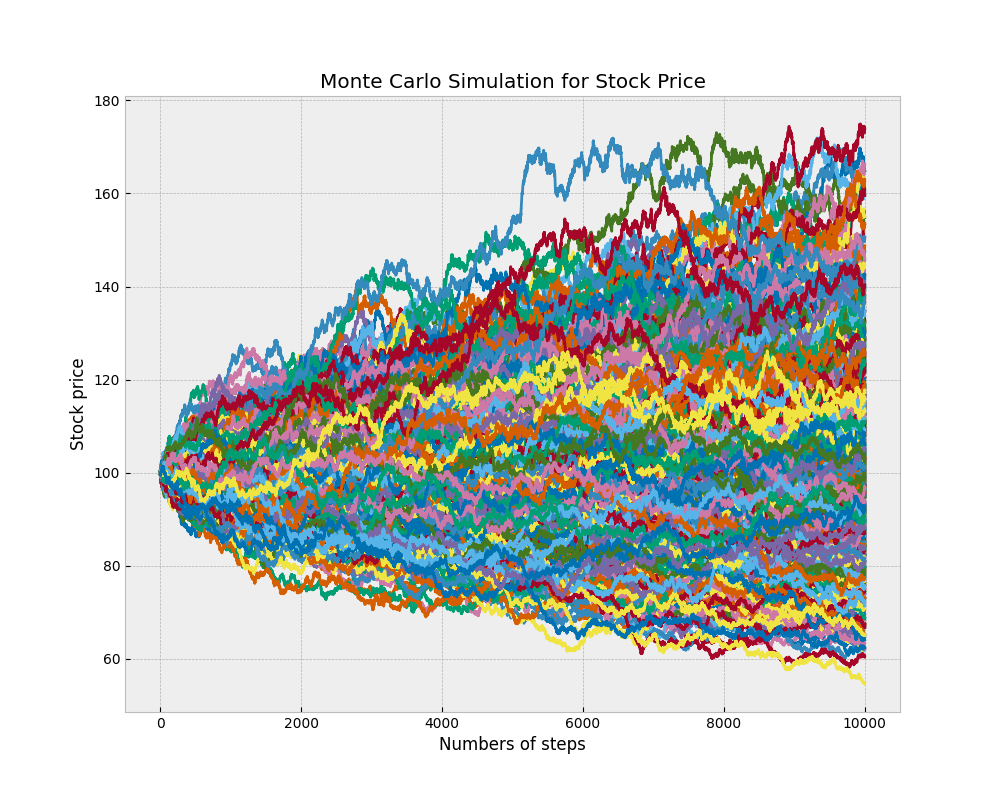

选择权定价

我们可以使用上述方法预测选择权到期时的股价，接著计算每个路径到期时的选择权内含价值，最后再回算内含价值现值后做平均就可以得到选择权理论价格。具体程式码请见下方:

def mc_options(CallOrPut, K, S0, r, sigma, T, Nsteps, Nrep):
    SPATH = mc_asset(S0, r, sigma, T, Nsteps, Nrep)
    if CallOrPut == 'call':
        payoffs = np.maximum(SPATH[:,-1] - K, 0)
        return np.mean(payoffs)*np.exp(-r*T)
    else:
        payoffs = np.maximum(K - SPATH[:,-1], 0)
        return np.mean(payoffs)np.exp(-rT)

其中我们可以使用 CallOrPut 参数调整选择权种类，我们带入数值后进行验算，并且比较使用 Black-Scholes 模型与 Greeks 所使用之方法下，所得理论价格是否有出路。

S0 = 100
K = 110
CallOrPut = 'put'
r = 0.03
sigma = 0.25
T = 0.5
Nsteps = 10000
Nrep = 1000
p_ = mc_options(CallOrPut, K, S0, r, sigma, T, Nsteps, Nrep)
mybs = BS_formula(S0, K, r, sigma, T)
c, p = mybs.BS_price()

print(f'Monte Carlo price: {c_}')
print(f'Black Scholes price: {p}')

所得结果如下图 2 所示，可以发现两者确实有些许差距但不大。

图 2: 蒙地卡罗与布莱克修斯模型比较

对偶变数法(Antithetic Variate)

由于蒙地卡罗模拟选择权价格就类似于生成大量可能的理论价格再进行平均，这样做必定会受到模拟出来价格波动度较大的问题，也就是模拟出来的价格可能会出现许多极端值，进而造成模拟结果失准。为了解决这项问题，我们可以采用对偶变数法降低波动度。其观念就是当我们生成一条股价路径(式 3)时，同时生成一个反向的报酬路径(式 4)，这时候两条路径的相关系数为 -1，造成两者相加所得的共变异数为最小，进而降低预估出选择权价格的波动度。

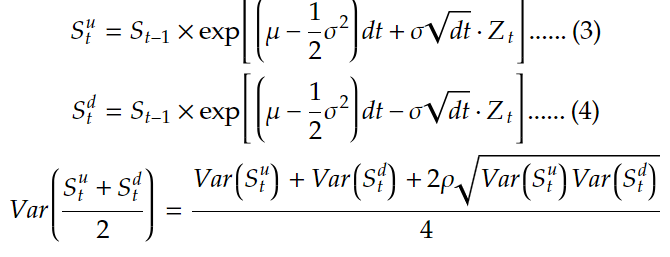
具体程式码编写如下，我们先生成两个矩阵进行计算，SPATH1 为第一个矩阵且为正向，SPATH2 则是反向所组成之矩阵，可以发现每次迭代生成随机乱数 (epsilon) 时，两个矩阵皆共享乱数，因此所需计算量降低并且降低选择权预测价格之波动程度。

def mc_options_AV(CallOrPut, K, S0, r, sigma, T, Nsteps, Nrep):

    SPATH1 = np.zeros((int(Nrep/2), 1 + Nsteps))
    SPATH2 = np.zeros((int(Nrep/2), 1 + Nsteps))
    SPATH1[:, 0], SPATH2[:, 0] = S0, S0
    dt = T / Nsteps
    nudt = (r - 0.5 * sigma **2) * dt
    sidt = sigma * np.sqrt(dt)
    
    for i in range(0,int(Nrep/2)):
        for j in range(0,Nsteps):
            epsilon = np.random.normal()
            SPATH1[i,j+1] = SPATH1[i,j] * np.exp(nudt + sidt * epsilon)
            SPATH2[i,j+1] = SPATH2[i,j] * np.exp(nudt - sidt * epsilon)
            
    if CallOrPut == 'call':
        C1 = np.maximum(SPATH1[:, -1] - K, 0)
        C2 = np.maximum(SPATH2[:, -1] - K, 0)
        C = np.mean(0.5 * (C1 + C2))
        C0 = np.exp(-r*T) * C
        return C0
    else: 
        P1 = np.maximum(K - SPATH1[:, -1], 0)
        P2 = np.maximum(K - SPATH2[:, -1], 0)
        P = np.mean(0.5 * (P1 + P2))
        P0 = np.exp(-r*T) * P
        return P0

接著代入数值检验在对偶变数法之下的选择权价格与一般蒙地卡罗之结果是否一致，结果请见图 3，可以得出确实十分接近。

CallOrPut = 'put'
K = 110
S0 = 100
r = 0.03
sigma = 0.25
T = 0.5
Nrep = 10000
Nsteps = 1000
print('Price under AV: ', mc_options_AV(CallOrPut, K, S0, r, sigma, T, Nsteps, Nrep))
print('Price under MC: ', mc_options(CallOrPut, K, S0, r, sigma, T, Nsteps, Nrep))

图 3: 对偶变数法与一般蒙地卡罗之比较

控制变数法(Control Variate)

除了对偶变数法以外，也可以透过控制变数法来降低选择权理论价格的波动程度。假设有一两随机变数 X 与 Y，其中 Y 变数平均数与变异数计算上十分容易。又假设两变数可以组成新变数 Z (式 5)，此时 Z 的期望值与 X 期望值相同(见式 6)，而变异数则由 c 决定，因此可以找出一个最佳的 c* 使 Z 的变异数达到最小，c* 最佳解如式 7。我们将 X、Y 视为每个路径上选择权与股票现货价格，我们使用过去选择权与股价的共变异数与股价之变异数计算最佳的 c*，接著再透过式 5 计算选择权理论价格 (E(Z))，就可以达成缩减蒙地卡罗波动度的目的。

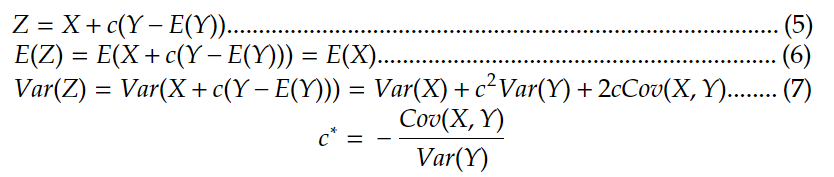
程式化结果如下方所表示:

CallOrPut: 选择权为买或卖权。
K: 履约价格。
S0: 期初价格。
r: 股价历史报酬。
sigma: 股价报酬波动度。
T: 到期时间。
Nsteps: 切分时间点数量。
Nrep: 路径数量。
Npilot: 计算 c* 所需之时间窗格。

def mc_options_CV(CallOrPut, K, S0, r, sigma, T, Nsteps, Nrep, Npilot):
    
    # Calculate covariance between stock and options price
    SPATH = np.zeros((Npilot, 1 + Nsteps))
    SPATH[:, 0] = S0
    dt = T / Nsteps
    nudt = (r - 0.5 * sigma **2) * dt
    sidt = sigma * np.sqrt(dt)
    
    for i in range(0,Npilot):
        for j in range(0,Nsteps):
            SPATH[i,j+1] = SPATH[i,j] * np.exp(nudt + sidt * np.random.normal())
    Sn = SPATH[:, -1] 
    if CallOrPut == 'call':
        Cn = np.maximum(SPATH[:,-1] - K, 0) * np.exp(-r*T)
        MatCov = np.cov(Sn, Cn)[0,1]
        VarY = S0 ** 2 * np.exp(2 * r * T) * (np.exp(T * sigma ** 2) - 1)
        c = -MatCov / VarY
        ExpY = S0 * np.exp(r*T)
    else:
        Pn = np.maximum(K - SPATH[:,-1], 0) * np.exp(-r*T)
        MatCov = np.cov(Sn, Pn)[0,1]
        VarY = S0 ** 2 * np.exp(2 * r * T) * (np.exp(T * sigma ** 2) - 1)
        c = -MatCov / VarY
        ExpY = S0 * np.exp(r*T)

    
    # Applying control variate function with optimal c*
    SPATH2 = np.zeros((Nrep, 1 + Nsteps))
    SPATH2[:, 0] =S0
    dt = T / Nsteps
    nudt = (r - 0.5 * sigma **2) * dt
    sidt = sigma * np.sqrt(dt)
    
    for i in range(0,Nrep):
        for j in range(0,Nsteps):
            SPATH2[i,j+1] = SPATH2[i,j] * np.exp(nudt + sidt * np.random.normal())
    S = SPATH2[:, -1] 
    if CallOrPut == 'call':
        C = np.maximum(SPATH2[:,-1] - K, 0) * np.exp(-r*T)
        CVC = np.mean(C + c * (S - ExpY))
        return CVC
    else:
        P = np.maximum(K - SPATH2[:,-1], 0) * np.exp(-r*T)
        CVP = np.mean(P + c * (S - ExpY))
        return CVP

透过代入数值，我们检验控制变数法与对偶变数法之下，所得的卖权价格结果如图 4，可发现几乎相同。

CallOrPut = 'put'
K = 110
S0 = 100
r = 0.03
sigma = 0.25
T = 0.5
Nrep = 5000
Nsteps = 1000
Npilot= 5000

print('Price under AV: ', mc_options_AV(CallOrPut, K, S0, r, sigma, T, Nsteps, Nrep))
print('Price under CV: ', mc_options_CV(CallOrPut, K, S0, r, sigma, T, Nsteps, Nrep, Npilot))

图 4: 对偶变数与控制变数法比较

实际案例

总结上述，我们学到了总共三种使用蒙地卡罗模拟计算选择权理论价格的方法，分别为: 一般法、对偶变数法与控制变数法，接著我们就导入真实案例，对比各方法的理论价格与 TEJ 所计算的 Black Sholes 价格是否有很大的差异。

S0 = stocks.loc['2023-01-31']['close_d']
K = 15500 
r = stocks['daily return'].rolling(252).mean().loc['2023-01-31'] # average return of stock
T = 51 / 252
sigma = stocks.loc['2023-01-31']['moving volatility'] * np.sqrt(252)
Nstep = 50000 
Nrep = 50000
Npilot = 5000
CallOrPut = 'put'

print('Monte Carlo theoretical price: ', mc_options(CallOrPut, K, S0, r, sigma, T, Nsteps, Nrep))
print('Monte Carlo with AV theoretical price: ', mc_options_AV(CallOrPut, K, S0, r, sigma, T, Nsteps, Nrep))
print('Monte Carlo with CV theoretical price: ', mc_options_CV(CallOrPut, K, S0, r, sigma, T, Nsteps, Nrep, Npilot))
print('TEJ Black Scholes price: ', puts.loc['2023-01-31']['theoremp'])
print('Real price: ', puts.loc['2023-01-31']['settle'])

我们采用时间为 2023-01-1 到 2023-04-19、履约价格为 15500 的台指卖权，Sigma 采用以 252 天为窗格的台指报酬率标准差，r 为最近 252 天的平均报酬率，且假设今日 2023 年 1 月 31 日。所得结果如下图 5，可以发现三种方法所得结果与 TEJ 计算的价格相比，都更趋近于实际价格。

结论

蒙地卡罗定价法相较于 CRR 模型与 Black-Scholes 模型，更仰赖大数法则，通过大量的股价路径，逐渐拟合到合理的理论价格。在这个电脑效能大幅进步的今天，这种资料驱动的演算法、定价模型相信只会越来越多。投资人在进行选择权投资时，不彷也将蒙地卡罗法也纳入考量。之后我们会提供更多选择权或衍生性商品相关的知识，欢迎持续关注本平台，此外，也欢迎读者及投资者们选购 TEJ E Shop 中的方案来建构自己的选择权定价程式。请注意以上订价公式与选择权商品仅为示范所用，不代表本台任何投资或标的上的建议。

完整程式码

点此前往Github