Photo by Isaac Smith on Unsplash
目录
首先,时间序列是按照时间轴排序,呈现历史数据发展过程的资料结构;而时间序列模型,则是依照上述资料结构分析其规律性以及趋势,并且透过找到概似的轨迹建立模型,用以预测未来的动向。
本系列所运用的模型:
整合移动平均自回归模型(Autoregressive Integrated Moving Average model, ARIMA model)
ARIMA是一个基础的时间序列模型,参数项目包括自我回归(AR)、差分次数(Differencing)以及移动平均数(MA)。
广义自回归条件异方差模型(General Autoregressive Conditional Heteroskedasticity model, GARCH model)
GARCH为分析时间序误差项目的模型,在金融领域的应用则是衡量资产或股价的波动度,本文会借由此模型检定ARIMA模型的残差项目,进行误差项目的修正。GARCH的参数项目与ARIMA的AR及MA不完全相同,GARCH是针对误差项以及变异数的模型,而在取用几个过往值这方面,本文会利用ACF/PACF图搭配GARCH模型本身特点决定(内文会再详细说明)。
本文流程:
本文使用 MacOS 并以 Jupyter Notebook作为编辑器
# 基本功能
import numpy as np
import pandas as pd# 绘图
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
sns.set()# TEJ API
import tejapi
tejapi.ApiConfig.api_key = 'Your Key'
tejapi.ApiConfig.ignoretz = True
证券交易资料表:上市(柜)未调整股价(日),资料代码为(TWN/EWPRCD)。
报酬率资讯表:上市(柜)股价报酬(日)-资料代码为(TWN/EWPRCD2)。
本文以元大台湾50指数作为标的。
data_price = tejapi.get('TWN/EWPRCD', # 公司交易资料-收盘价
coid= '0050', # 台湾50
mdate={'gte': '2003-01-01', 'lte':'2021-12-24'},
opts={'columns': ['coid', 'mdate', 'close_d', ]},
chinese_column_name=True,
paginate=True)
data_price = data_price.set_index('日期')# 导入中文
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS']# 绘制0050价格走势图
fig, ax = plt.subplots(figsize = (10, 5))
plt.plot(data_price['收盘价'], label = '0050-price')
plt.title('0050收盘价')
plt.legend()
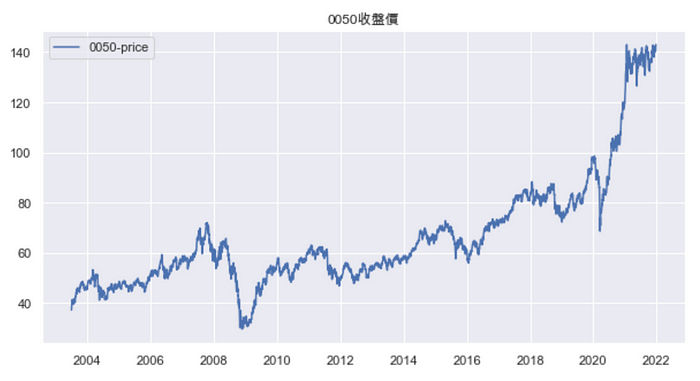
根据上图可以发现,0050的价格随著时间推移,有明显的波动,而这样的情形有可能源于该数据为非定态,所以这边会操作Augmented Dickey-Fuller(ADF)检定数列是否存在单位根,若数列存在单位根通常代表其为非平稳数列,可以透过取差分的方式转换成平稳数列。本文将透过P-value验证其定态与否。
# 从statsmodels数据包导入ADF套件
from statsmodels.tsa.stattools import adfuller# 从产出的ADF报表撷取P-value项目
price_p_value = adfuller(data_price['收盘价'])[1]# 设定判别式以及0.05的P-value标准
if price_p_value > 0.05:
print('Nonstationary')
else:
print('Stationary')
H0:非定态资料
H1:定态资料

透过ADF检定可以知道股价数据确实是非定态的资料,所以并不能够以此为模型的数据来源。
此处需说明定态的重要性是因为当资料为非定态时,则其波动走势为随机漫步,因此,即便后续模型能够有很好的配适,那也只是刚好的结果,并不能说明模型的强度,毕竟随机波动没办法用模型来解释。
在说明无法运用价格资料作为模型的依据后,本文导入报酬率资料。(绘图与ADF检定过程详见完整程式码)
data_ret = tejapi.get('TWN/EWPRCD2', # 公司交易资料-报酬率
coid= '0050', # 台湾50
mdate={'gte': '2003-01-01', 'lte':'2021-12-24'},
opts={'col umns': ['coid', 'mdate', 'roia', ]},
chinese_column_name=True,
paginate=True)
data_ret = data_ret.set_index('日期')
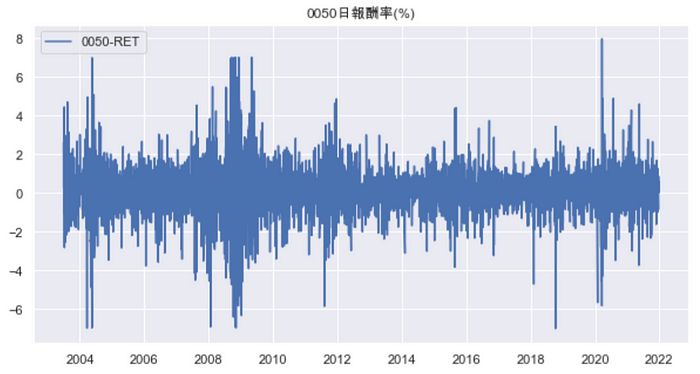

透过ADF检定可以知道报酬率数据是定态的资料,所以能够以此为模型的数据来源。
train_date = data.index.get_level_values('日期') <= '2020-12-31'
train_data = data[train_date]
test_data = data[~train_date]
以train_data的期间建立模型,并以test_data的期间作为模型的测试,并与实际资料做比对,而本文为数据前处理以及模型基本建置的说明,所以并不会运用到test_data的资料。
本文用pmdarima套件找出最佳的参数组合。
import pmdarima as pmdpmd_mdl = pmd.auto_arima(train_data['日报酬率(%)'], stationary = True)
pmd_mdl.summary()

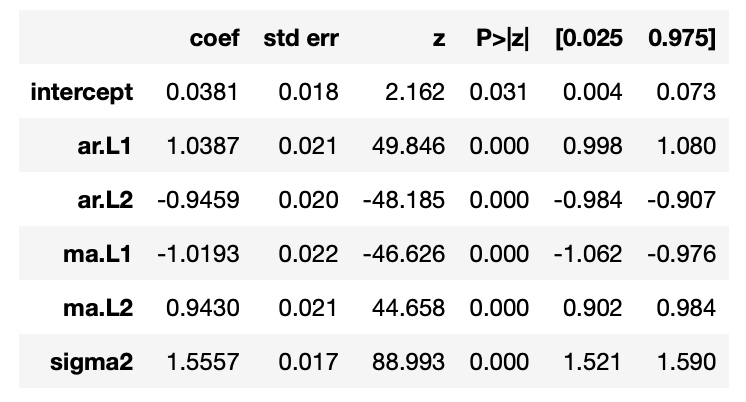
通过报表,得知pmdarima所提供的最佳参数组合为(2, 0, 2);此外,也可以从参数估计报表中得知每项P-value皆小于0.01的最严格标准,所以各参数的显著水准也没有问题。(读者若注意到左上报表中的模型名称是SARIMAX而非ARIMA,可以不用担心,这是套件预设的名称,若仍不放心可以导入另一个套件检查各项数值。)
from statsmodels.tsa.arima.model import ARIMAmodel = ARIMA(train_data['日报酬率(%)'], order = (2, 0, 2))
stats_mdl = model.fit()
print(stats_mdl.summary())
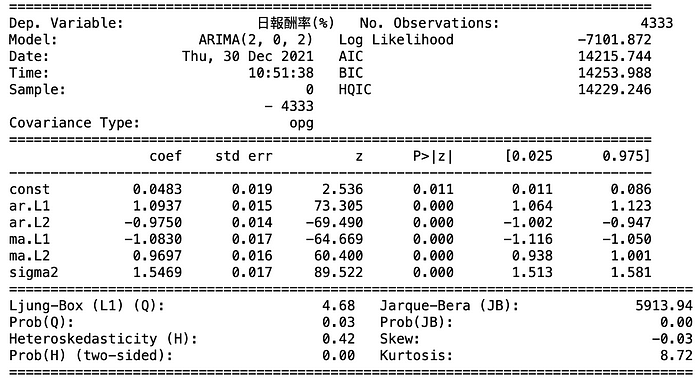
观察新的套件产出的ARIMA模型报表,可以看到在模型配适标准值(AIC或BIC)上与先前的报表相差不远;并且在参数估计值报表的部分,尽管估计值以及标准差有些许不同,但也不影响P-value在显著性上的结果,所以不必太纠结于此。
stats_mdl.plot_diagnostics(figsize = (15, 10))
plt.show()
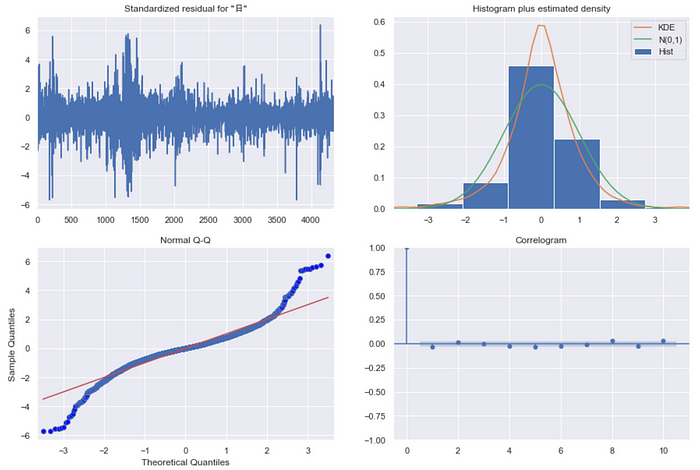
从上图残差诊断可以目测残差(左上)无明显的趋势,但是观察残差直方图(右上)却发现具有窄峰厚尾的现象,代表不符合回归常态假设;并且从常态机率图(左下)来看,模型残差的常态性不足,所以ARIMA模型的残差项应该还有潜在的解释变量,以下将进行白噪音检定进一步确认。
借由Ljung-Box检定观察ARIMA模型的残差项是否为随机变动,若检定结果呈现白噪音(随机),则可以知道ARIMA模型的配适程度良好,便直接做预测;然而,若检定结果呈现误差项目并非白噪音,则需要用GARCH模型找出误差项中的变异数解释变量。
from statsmodels.stats.diagnostic import acorr_ljungboxwhite_noise = acorr_ljungbox(pmd_residual, lags = [10], return_df=True)
H0:误差项为白噪音
H1:误差项非白噪音
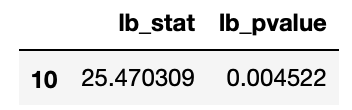
检定结果让我们能够以P-value判断,此误差项并不是白噪音(P-value < 0.05),所以本文后续会执行GARCH模型适配ARIMA的残差项目。
首先,尽管本文已经透过白噪音检定了解ARIMA模型在误差的问题,然而若要证明该项目有变异数异质性,还须进行ARCH Effect Test确认。
from statsmodels.stats.diagnostic import het_archLM_pvalue = het_arch(arima_resid, ddof = 4)[1]
print('LM-test-Pvalue:', '{:.5f}'.format(LM_pvalue))
H0:不具有ARCH Effect
H1:具有ARCH Effect
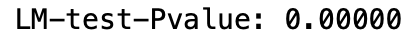
透过检定结果的P-value可以拒绝虚无假设,也就说明ARIMA的误差项可以进行GARCH模型修正。
透过观察残差ACF/PACF图,了解残差平方项目的滞后情形,并将观察到的结果带入GARCH模型中,决定GARCH模型的参数组合,检定波动度。
fig, ax = plt.subplots(1, 2, figsize = (18,5))pmd_residual = pmd_mdl.arima_res_.resid
sgt.plot_acf(pmd_residual**2, zero = False, lags = 40, ax=ax[0])
sgt.plot_pacf(pmd_residual**2, zero = False, lags = 40, ax=ax[1])plt.show()
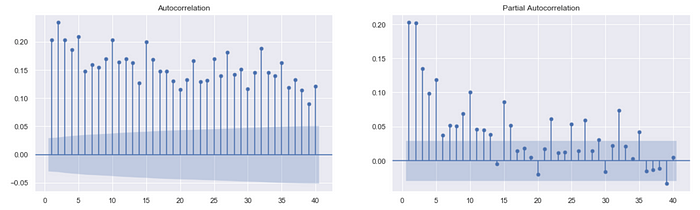
从图中了解残差平方的自回归程度很大,而综合考量PACF图(右上)中第一、二期的滞后较明显以及GARCH模型数学式结构,本文假设参数组合(p,q)为(1,1)、(2,1)、(1,2)、(2,2),并互相比较配适程度以及各参数项系数的显著水准,然后才决定使用哪个组合。本文因应篇幅考量,所以只展示最适组合(1,1)。
Note: GARCH模型数学式结构会直接包含过往各期值,而距离时间越远系数权重越低。
from arch import arch_modelmdl_garch = arch_model(pmd_residual, vol = 'GARCH', p = 1, q = 1)
res_fit = mdl_garch.fit()
res_fit.summary()


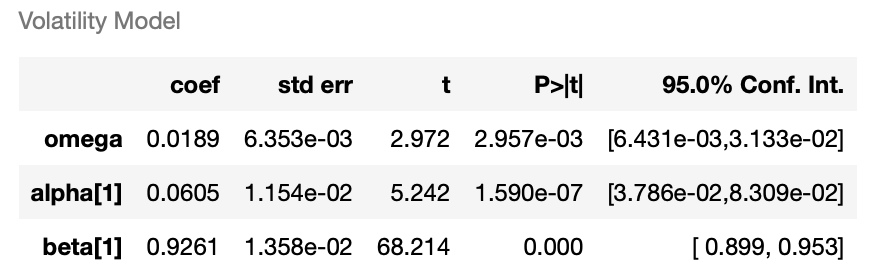
借由观察上表,了解各项参数估计值皆具备显著水准,以下将进行模型诊断,验证GARCH模型的残差项为随机变量。


从上图残差诊断目测残差无明显的趋势,而从残差直方图(右下)也可以发现其概似常态分配;此外,观察常态机率图(左下),模型残差的常态性也足够,所以GARCH模型的残差项应该没有潜在的解释变量,以下将进行白噪音检定进一步确认。
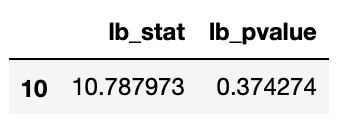
检定结果让我们能够以P-value判断,此误差项是白噪音(P-value > 0.05),代表残差项目中没有其他解释变量可以提取,已经是随机过程。
至此,本文已经将模型建置的整体流程展示一遍,从最初的数据定态分析,接著导入ARIMA模型找出需要套用的历史资料组合(AR与MA项目),最后将ARIMA项目的残差套入GARCH模型进行误差修正。此外,读者应该也发现统计学在处理数据上是非常严谨的,而本文为了提高易读性,亦省略检定背后的数学过程,让读者快速了解整个流程。
以上就是本文想要让读者了解的时间序列模型建置,续篇文章将说明如何运用本文得到的模型,进行走势预测。最后要提醒读者,本文在处理数据上较方便是因为TEJ数据库的资料齐全,所以欢迎对金融数据分析有兴趣的读者,至TEJ E-Shop选购符合自身需求的资料包组合。

电子报订阅