
目录
1997年诺贝尔经济学奖,在众多入围者中,Robert Merton 与 Myron Scholes 凭借著 Black-Scholes options pricing formula 喜提金杯。Black-Scholes 模型也凭著其优秀的数学性质、简易且易用的特性,至今仍是金融机构或投资人爱用的选择权定价模型。今天我们就是要针对该模型进行程式化,并且介绍与程式化其衍生的 Greeks。
本文使用 Window 作业系统以及 Jupyter Notebook 作为编辑器。
# 载入所需套件
import math
import tejapi
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
plt.style.use('bmh')
plt.rcParams['font.sans-serif']=['Microsoft YaHei']
# 登入TEJ API
api_key = 'YOUR_KEY'
tejapi.ApiConfig.api_key = api_key
tejapi.ApiConfig.ignoretz = True公司交易面资料库: 未调整股价(日),资料代码为(TWN/APRCD)。
衍生性金融商品资料库: 选择权日交易状况,资料代码为(TWN/AOPTION)。
使用台湾加权股价指数(Y9999)未调整收盘价,时间区间为2021/03/16到2023/04/10。并且载入台湾加权指数买权(TXO202304C15500),该选择权为欧式买权、开始交易日为3/16,到期日为4/19,履约价格为15500。
gte, lte = '2021-03-16', '2023-04-10'
# 标的物价格
stocks = tejapi.get('TWN/APRCD',
paginate = True,
coid = 'Y9999',
mdate = {'gte':gte, 'lte':lte},
chinese_column_name = True,
opts = {
'columns':[ 'mdate','close_d']
}
)
# 选择权价格
options = tejapi.get(
'TWN/AOPTION',
paginate = True,
coid = 'TXO202304C15500',
mdate = {'gte':gte, 'lte':lte},
chinese_column_name = True,
opts = {
'columns':['mdate', 'coid','settle', 'kk', 'theoremp', 'acls', 'ex_price', 'td1y', 'avolt', 'rtime']
}
)
# 重设日期为index
stocks = stocks.set_index('年月日')
options = options.set_index('日期')计算大盘之日报酬并且计算移动报酬波动度,以252天也就是一年为窗格迭代下去。
stocks['日报酬'] = np.log(stocks['收盘价(元)']) - np.log(stocks['收盘价(元)'].shift(1))
stocks['移动报酬波动度'] = stocks['日报酬'].rolling(252).std()所得标的物价格表格如下:
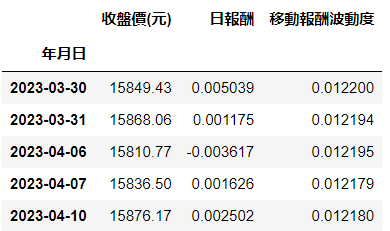
接著进行 Black Scholes formula 程式化,我们先看一下Black Scholes formula 长甚么样子。
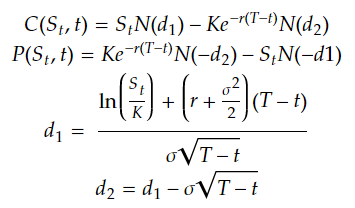
其中:
● C(St,t), P(St,t) : 表示第t日的买、卖权理论价格。
● St, K : 表示第t日标的物价格与履约价格。
● T, t : 表示选择权时间长度与第t天。
● sigma : 表示历史报酬波动度,这里采过去252日的报酬计算波动度。
● r : 表示无风险利率。
● N() : 标准常态分配的累积机率密度函数。
若观察上述式子可以发现,影响买卖权理论价格的因素不外乎这五个: 标的物价格、履约价格、剩余到期天数(T-t)、报酬波动度与无风险利率。除了履约价格外,其他因素都会随著时间推移而产生变化,而财金学家为了探讨这四个因素与买卖权价格间的连动,发明了 Greeks 来量化四个因素与价格间的关系。分别为 delta、gamma、vega、theta 与 rho。
而这五个 greeks 就是让选择权价格分别对标的物价格、波动度、剩余到期时间与无风险利率做微分,而gamma是选择权价格对标的物价格作两次微分。有赖于先人的努力,每个 greeks 都有解析解,让我们不用处理讨厌的偏微分方程式😆。以下公式,从上到下就是买权delta →卖权delta →买、卖权gamma →买、卖权vega →买权theta →卖权theta →买权rho →卖权rho的解析解。
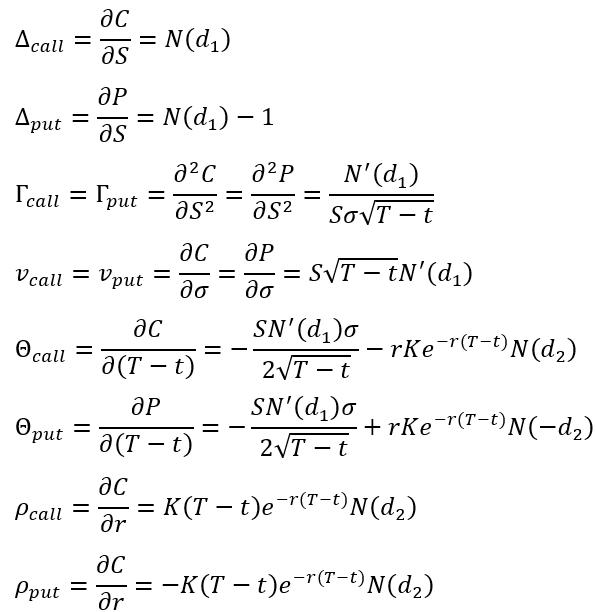
废话不多说,直接上code 😎。
class BS_formula:
def __init__(self, s0, k, r, sigma, T):
self.s0 = s0 # 标的物价格
self.k = k # 履约价格
self.r = r # 无风险利率
self.sigma = sigma # 历史波动度
self.T = T # 剩余到期时间
self.d1 = (np.log(s0/k)+(r+sigma**2/2)*T) / (sigma * np.sqrt(T))
self.d2 = ((np.log(s0/k)+(r+sigma**2/2)*T) / (sigma * np.sqrt(T))) - sigma*np.sqrt(T)
def BS_price(self): # 计算理论价格
c = self.s0*norm.cdf(self.d1) - self.k*np.exp(-self.r*self.T)*norm.cdf(self.d2)
p = self.k*np.exp(-self.r*self.T)*norm.cdf(-self.d2) - self.s0*norm.cdf(-self.d1)
return c,p
def BS_delta(self): # 计算 delta
return norm.cdf(self.d1), norm.cdf(self.d1)-1
def BS_gamma(self): # 计算 gamma
return norm.pdf(self.d1)/(self.s0*self.sigma*np.sqrt(self.T)), norm.pdf(self.d1)/(self.s0*self.sigma*np.sqrt(self.T))
def BS_vega(self): # 计算 vega
return self.s0*np.sqrt(self.T)*norm.pdf(self.d1), self.s0*np.sqrt(self.T)*norm.pdf(self.d1)
def BS_theta(self): # 计算 theta
c_theta = -self.s0*norm.pdf(self.d1)*self.sigma / (2*np.sqrt(self.T)) - self.r*self.k*np.exp(-self.r*self.T)*norm.cdf(self.d2)
p_theta = -self.s0*norm.pdf(self.d1)*self.sigma / (2*np.sqrt(self.T)) + self.r*self.k*np.exp(-self.r*self.T)*norm.cdf(-self.d2)
return c_theta, p_theta
def BS_rho(self): # 计算 rho
return self.k*self.T*np.exp(-self.r*self.T)*norm.cdf(self.d2), -self.k*self.T*np.exp(-self.r*self.T)*norm.cdf(-self.d2)接著我们用上述公式,在给定其他条件下,以视觉化方式观察标的物价格对买卖权价格之影响。可以发现买权与卖权价格大致呈现对称,买权价格与标的物价呈现正向变动,而卖权价格与标的物价呈现反向变动。除此之外,我们可以发现持有买权之下,具有风险有限、增值无限的特性,因为当深价外时,选择权价值至多减损至0,然而深价内时报酬可趋近于无限。而持有卖权虽风险有限,但受限于标的物价格至多减损到0,故报酬无法达成无限。
s0 = np.linspace(200,800)
k = 500
r = 0.00
sigma = 0.2
T = 252/252
mybs = BS_formula(s0, k, r, sigma, T)
c, p = mybs.BS_price()
fig = plt.figure(figsize = (12,8))
plt.plot(s0, c, label = '买权')
plt.plot(s0, p, label = '卖权')
plt.axvline(x = 500, color = 'black', linestyle = '--')
plt.xlabel('标的物价格', fontsize = 15)
plt.ylabel('选择权价格', fontsize = 15)
plt.title('选择权价格 VS. 标的物价格', fontsize = 20)
plt.legend(fontsize = 14)
plt.savefig('black scholes put call price.png')
plt.show()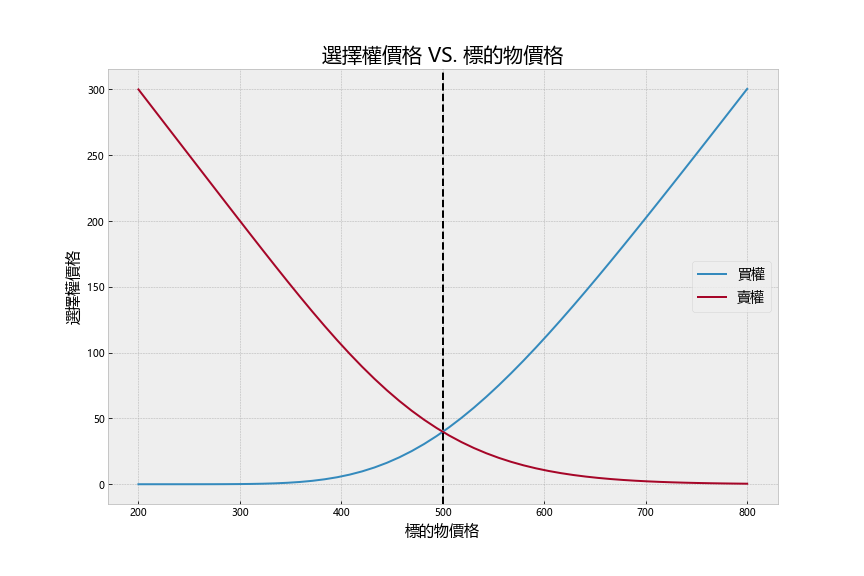
接著是看看画出给定其他条件之下,不同履约价格与Delta之间的关系图。delta在财务上的意义为每当标的物价格增加一单位,选择权价格的增减量。可以发现在深价外时,买卖权的delta都趋近于0;深价内时,买权趋近于1、卖权趋近于-1。代表在深价外时,小幅的标的物价格变动对于选择权价格是没啥影响;在深价内时,小幅的标的物价格变动则会造成选择权价格有较大的波动且波动幅度与标的物波动幅度相当。
s0 = np.linspace(200,800)
k = 500
r = 0.00
sigma = 0.2
T = 252/252
mybs = BS_formula(s0, k, r, sigma, T)
c, p = mybs.BS_delta()
fig = plt.figure(figsize = (12,8))
plt.plot(s0, c, label = '买权')
plt.plot(s0, p, label = '卖权')
plt.axvline(x = 500, color = 'black', linestyle = '--')
plt.axhline(y = 0, color = 'black', linestyle = '--')
plt.xlabel('标的物价格', fontsize = 15)
plt.ylabel('Delta值', fontsize = 15)
plt.title('Delta值 VS. 标的物价格', fontsize = 20)
plt.legend(fontsize = 14)
plt.savefig('black scholes put call delta.png')
plt.show()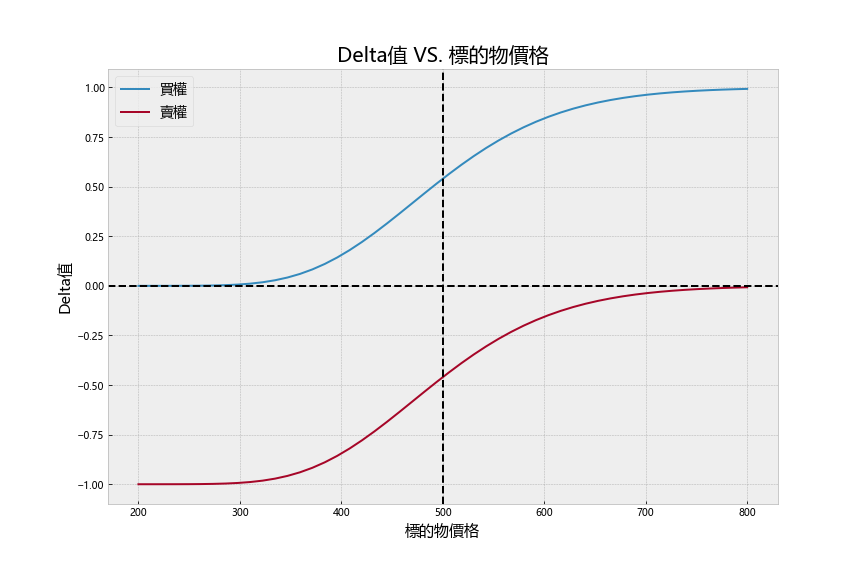
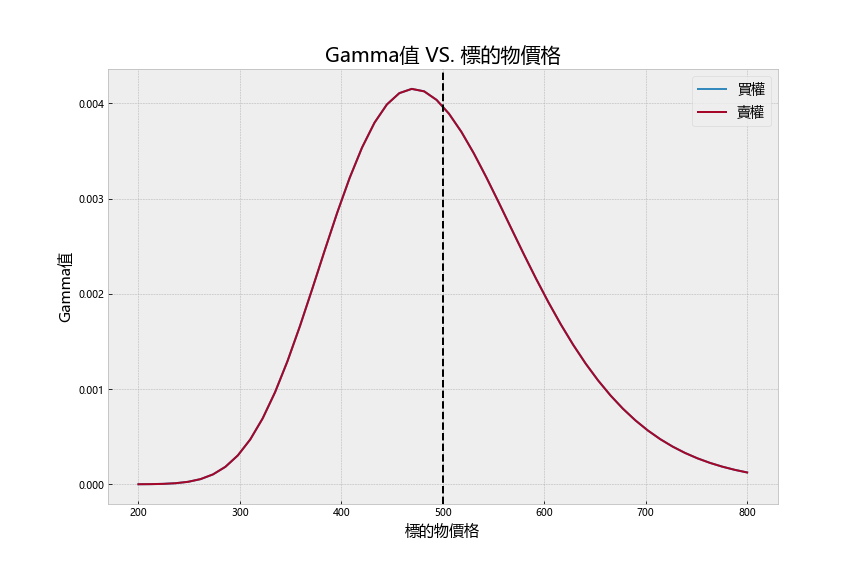
gamma是标的物价格对选择权价格的二次微分,可以理解为delta曲线的斜率,也就是在不同标的物价格之下,delta的增长速度。在给定其他条件下,可以视觉化 gamma 与标的物价格之关系。可以发现卖买权的gamma是一样的,且在约价平时,gamma最大,表示若从深价外走到深价内时,delta的增长幅度会是递增然后递减。程式码请见文末。
我们也可以观察价内、平与外的选择权在不同到期日之下,gamma 的变化。可以发现在价平且快到期时,gamma值窜升得不可思议。这就是鼎鼎大名的 gamma risk,也就是说快到期时,价平选择权的价格波动往往很大,许多风险趋避较深的投资人往往在快到期时,就会将持有选择权部位平仓。但也是有些人会反向操作,在快到期时买入,以较大的 gamma 拚搏较大的风险溢酬。
s0, s1, s2 = 400, 500, 600
k = 500
r = 0.00
sigma = 0.2
T = np.linspace(1, 0.01)
mybs0 = BS_formula(s0, k, r, sigma, T)
c0, p0 = mybs0.BS_gamma()
mybs1 = BS_formula(s1, k, r, sigma, T)
c1, p1 = mybs1.BS_gamma()
mybs2 = BS_formula(s2, k, r, sigma, T)
c2, p2 = mybs2.BS_gamma()
fig = plt.figure(figsize = (12,8))
plt.plot(T, c0, label = '买权(价外)')
plt.plot(T, c1, label = '买权(价平)')
plt.plot(T, c2, label = '买权(价内)')
plt.xlabel('剩余时间', fontsize = 15)
plt.ylabel('Gamma值', fontsize = 15)
plt.title('Gamma值 VS. 剩余时间', fontsize = 20)
plt.legend(fontsize = 14)
plt.axis([1.005, -0, -0.005, .045])
plt.savefig('black scholes put call gamma2.png')
plt.show()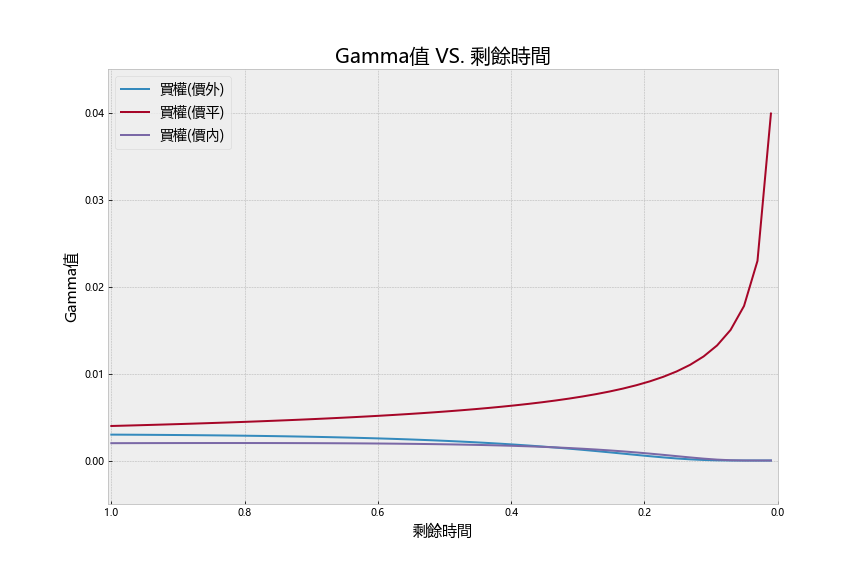
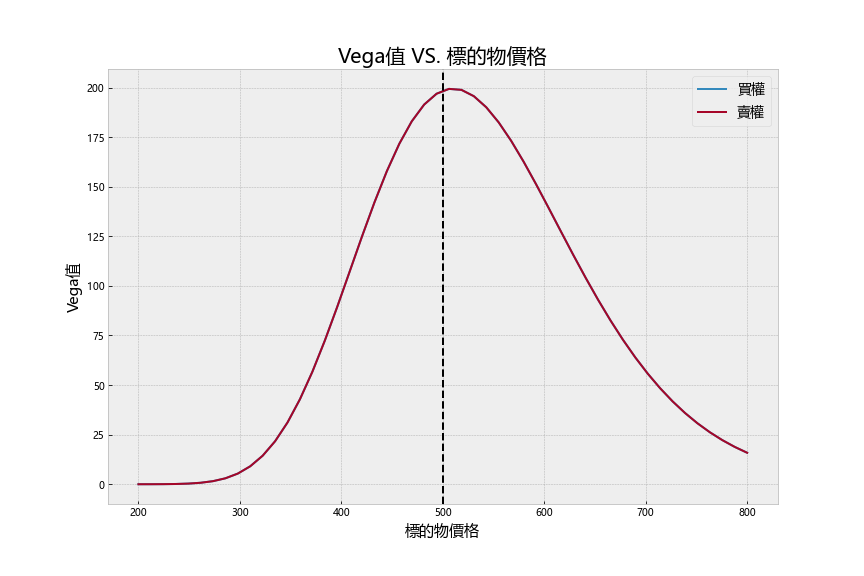
与 Gamma 相似,买卖权的 vega 基本上是相同的。vega 是当波动度增加一单位时,选择权价格的变动幅度。从下图可以发现当价平附近时,vega值达到最大,表示在价平时,选择权价格最容易受到波动度影响。程式码请见文末。
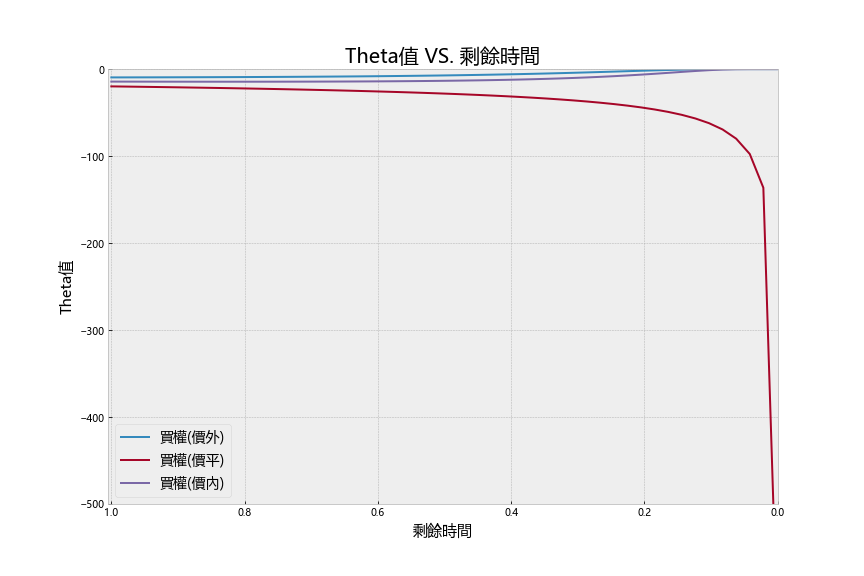
theta 为每单位时间增加,选择权价值变化的幅度。我们可以绘制一张在不同标的物价格且其他条件固定下,Theta值的变化图。可以发现在深价内或价外时,Theta在快靠近到期日时,都会趋近于0;反之,价平却有一个极大的向下幅度。可以注意到 theta 一直都为负值,是因为随著时间移动,选择权的时间价值会逐渐衰减。程式码见文末。
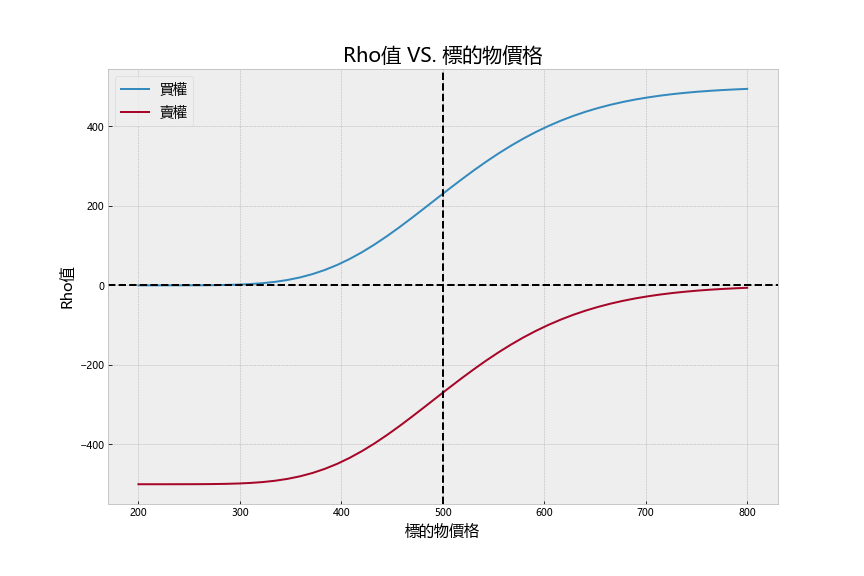
最后我们将每单位无风险利率移动,造成选择权价格移动的幅度,称之为Rho。我们可以将 Rho 与标的物价格绘图,可以发现随著标的物价格上升,Rho值会越来越大。程式码见文末。
接著我们使用台指买权作为举例,计算出在履约价格为15500元,到期日为四月之下,4/10 的买权理论价格,并且比较实际价格的差异。
r = 0.012
s0 = stocks.loc['2023-04-10']['收盘价(元)']
k = 15500
sigma = stocks.loc['2023-04-10']['移动报酬波动度']*np.sqrt(252)
T = 6/252
mybs = BS_formula(s0, k, r, sigma, T)
c, p = mybs.BS_price()
c_delta, p_delta = mybs.BS_delta()
c_gamma, p_gamma = mybs.BS_gamma()
c_vega, p_vega = mybs.BS_vega()
c_theta, p_theta = mybs.BS_theta()
c_rho, p_rho = mybs.BS_rho()
print('==2023-04-10履约价为525的台积电买权==')
print('当前标的物价格为 %.3f, 年化波动度为 %.3f, 剩余期间为 %.3f'%(s0, sigma, T*252))
print('买权理论价格: %.4f, 卖权理论价格: %.4f' %(c,p))
print('买权delta: %.4f, 卖权delta: %.4f' %(c_delta,p_delta))
print('买权gamma: %.4f, 卖权gamma: %.4f' %(c_gamma,p_gamma))
print('买权vega: %.4f, 卖权vega: %.4f' %(c_vega,p_vega))
print('买权theta: %.4f, 卖权theta: %.4f' %(c_theta,p_theta))
print('买权rho: %.4f, 卖权rho: %.4f' %(c_rho,p_rho))
options.loc['2023-04-10'] # 实际买权价格

比较我们算出的理论价格与结算价格,可以发现有不小的差距(435.54 – 385),表示目前买权可能是低估的。除此之外,TEJ API 在衍生性金融商品资料库中,也有提供理论价格的服务。TEJ API 所算的理论价格与我们的有些许的差距(440.36 v.s. 435.54),有可能是因为计算历史波动度的方法不同或是采用不同的无风险利率标准。
温馨提醒,本次介绍与标的仅供参考,不代表任何商品或投资上的建议。之后也会介绍使用TEJ资料库来建构各式选择权模型,所以欢迎对选择权交易有兴趣的读者,选购TEJ E-Shop的相关方案,用高品质的资料库,建构出适合自己的订价模型。

电子报订阅