CRR模型

May 30 2023

本文重点概要

文章难度：★★★☆☆
使用交易面资料进行选择权定价
阅读建议：本文主要将 CRR Model 程式化，公式的推导并不在这次文章的范畴内，建议读者再阅读前，先了解 CRR Model 的意涵。

前言

在我们之前的文章 — Black-Scholes 模型与 Greeks，向各位介绍了如何将 Black-Scholes Model 程式化，然而 Black-Scholes 模型无法推算美式买卖权的理论价格，因此在 Black Scholes 横空出世的三年后，约翰考克斯、史蒂芬罗斯与马克史宾斯坦发明了一个相对简易但更泛用的选择权定价公式 — CRR 模型。

CRR 模型利用离散二项式定理，假使未来每个时间点都只会有上涨与下跌两种情况，并且涨幅跌幅固定。如此一来，未来标的物价格就可以随时间推进绘制成一张二元树模型。接著计算每个节点之下，选择权的内含价值，再将每节点的价值取其现值后，向前推导就可以得出选择权的理论价值。

编辑环境与模组需求

本文使用 Window 作业系统以及 Jupyter Notebook 作为编辑器。

# Load required package
import math 
import tejapi
import pandas as pd 
import numpy as np 
import matplotlib.pyplot as plt 
from scipy.stats import norm
plt.style.use('ggplot')

# log in TEJ API
api_key = 'YOUR_KEY'
tejapi.ApiConfig.api_key = api_key
tejapi.ApiConfig.ignoretz = True

资料库使用

公司交易面资料库: 未调整股价(日)，资料代码为(TWN/APRCD)。
衍生性金融商品资料库: 选择权日交易状况，资料代码为(TWN/AOPTION)。

资料导入

使用台湾加权股价指数(Y9999)未调整收盘价，时间区间为2021/01/31到2023/04/19。并且载入台湾加权指数买权与卖权(TXO202304C15500、TXO202304P15500)，该选择权为欧式买权、开始交易日为1/31，到期日为4/19，履约价格为15500。

# set time zone
gte, lte = '2021-03-16', '2023-04-20'

# Get stock price
stocks = tejapi.get('TWN/APRCD',
                   paginate = True,
                   coid = 'Y9999',
                   mdate = {'gte':gte, 'lte':lte},
                   opts = {
                       'columns':[ 'mdate','close_d']
                   }
                  )

# Get options price
puts = tejapi.get( # puts price
    'TWN/AOPTION',
    paginate = True,
    coid = 'TXO202304P15500',
    mdate = {'gte':gte, 'lte':lte},
    opts = {
        'columns':['mdate', 'coid','settle', 'kk', 'theoremp', 'acls', 'ex_price', 'td1y', 'avolt', 'rtime']
    }
)
calls = tejapi.get( # calls price
    'TWN/AOPTION',
    paginate = True,
    coid = 'TXO202304C15500',
    mdate = {'gte':gte, 'lte':lte},
    opts = {
        'columns':['mdate', 'coid','settle', 'kk', 'theoremp', 'acls', 'ex_price', 'td1y', 'avolt', 'rtime']
    }
)

# set index
stocks = stocks.set_index('mdate')
puts = puts.set_index('mdate')
calls = calls.set_index('mdate')

资料处理

计算大盘之日报酬并且计算移动报酬波动度，以252天也就是一年为窗格迭代下去。

# Calculate stock return and moving volatility
stocks['daily return'] = np.log(stocks['close_d']) - np.log(stocks['close_d'].shift(1))
stocks['moving volatility'] = stocks['daily return'].rolling(252).std()

CRR 模型

如同前言所述，CRR 模型是一个更直观且更灵活的选择权定价模型。虽然他不像 Black Scholes 一样具有封闭解，且因为二元树结构的关系，在计算上会较 Black Scholes 耗时。然而，CRR 因为会遍历选择权存续的所有时间点，因此在针对一些因时而变的选择权定价上，相较于Black Scholes更有优势，比如: 美式选择权、奇异选择权。

CRR 模型的公式基本上就是针对二元树每个节点进行求现值的动作，一开始我们可以利用以下公式计算出下一个时间点，股价涨跌的幅度与机率，分别为图中的u, d, p。

接著可以计算出下个时点上升与下降的股价，并且随著时间推移形成一个树状图。图中黑色的线条与数学式为股价的变化，而红色的线条与数学式则是买权的价值。可以发现我们先算出未来股价的变化(EX: uS0, dS0)，再来将股价与履约价格相减取得买权的内含价值(EX: Ct,1, Ct,2)，最后将买权内含价值一步一步回推现值，最终可推回今日买权理论价格。

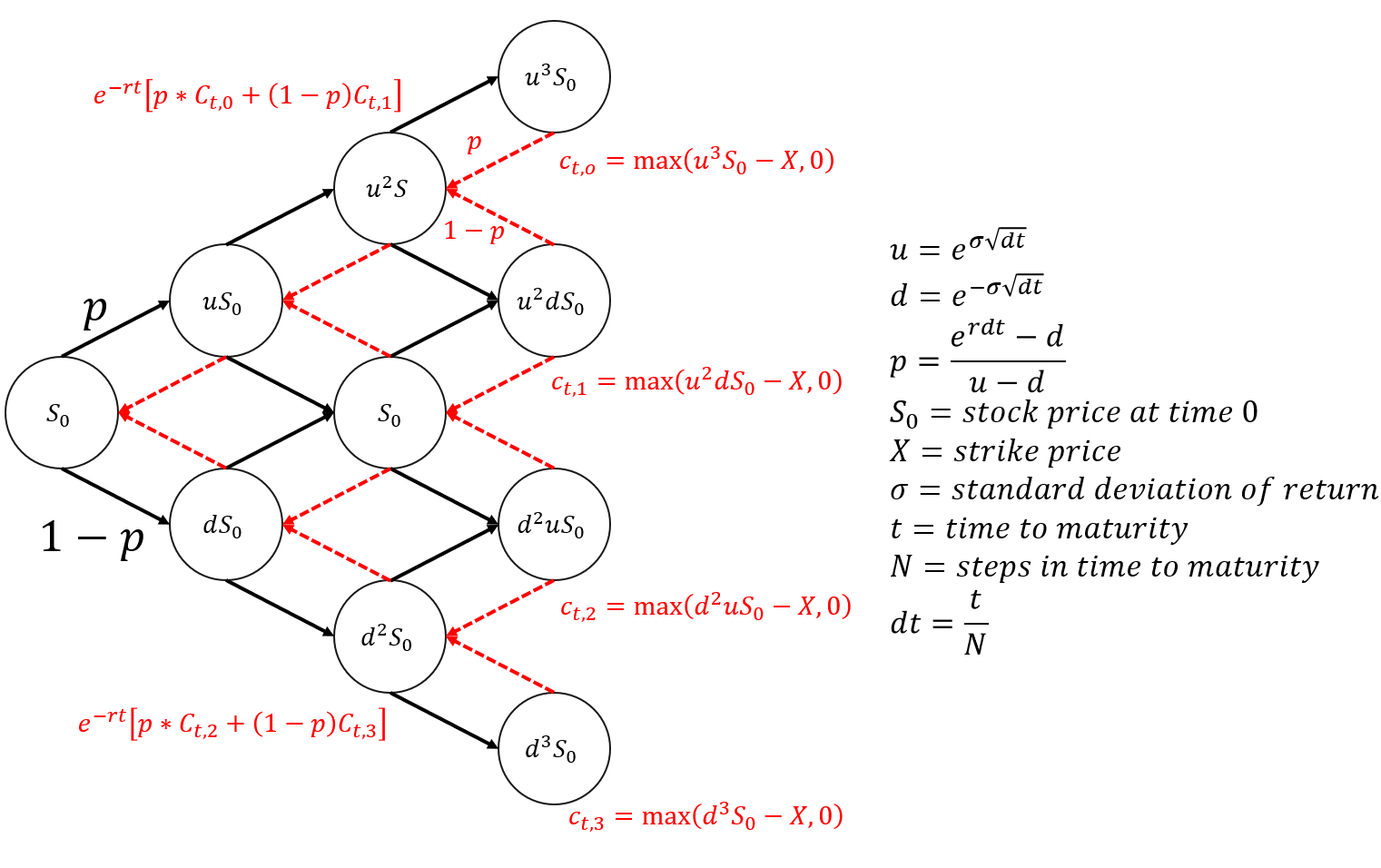
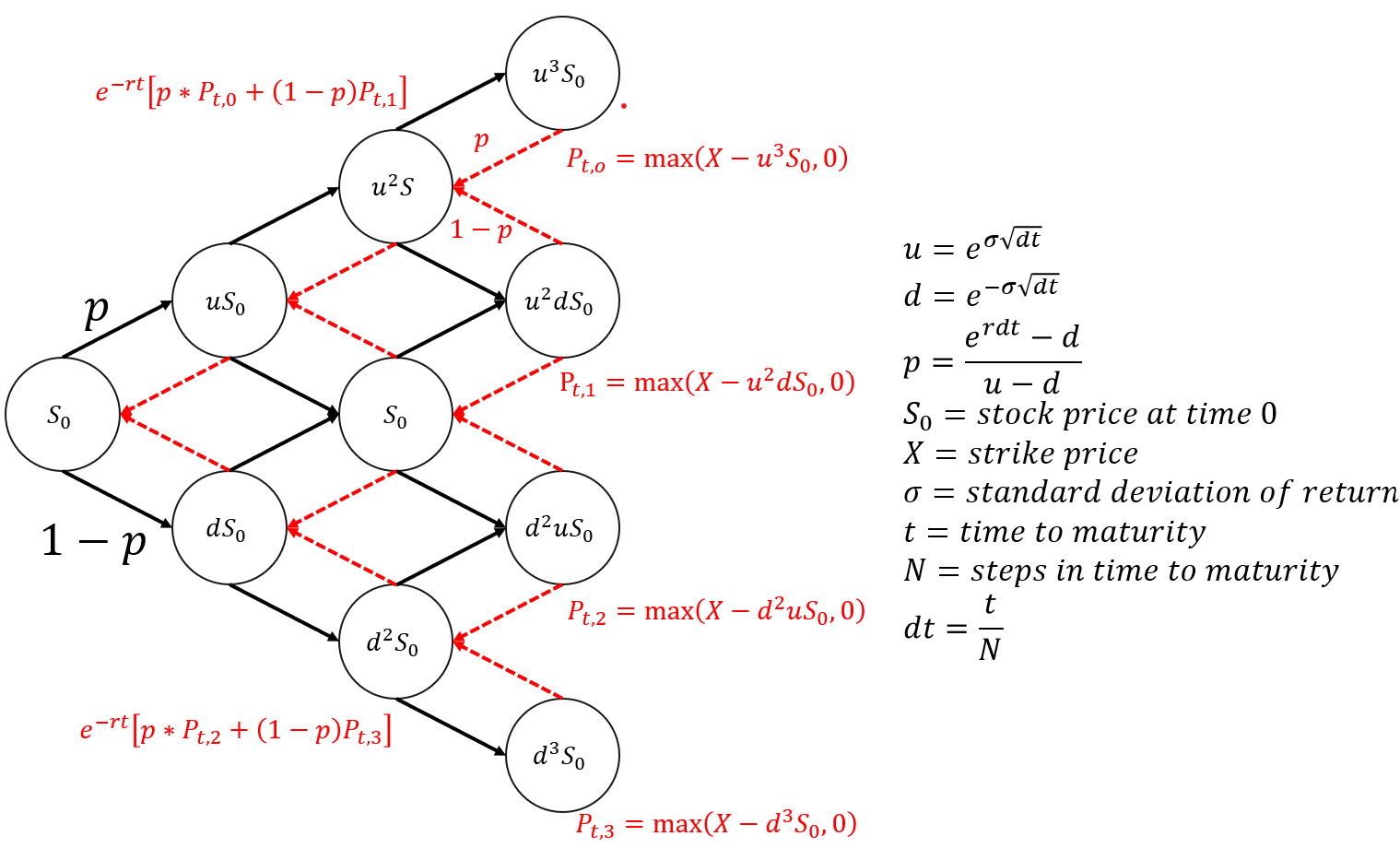
卖权的话则只需要改变计算内含价值的方法，改动为履约价格扣除股票价格(EX: Pt,0, Pt,1)。

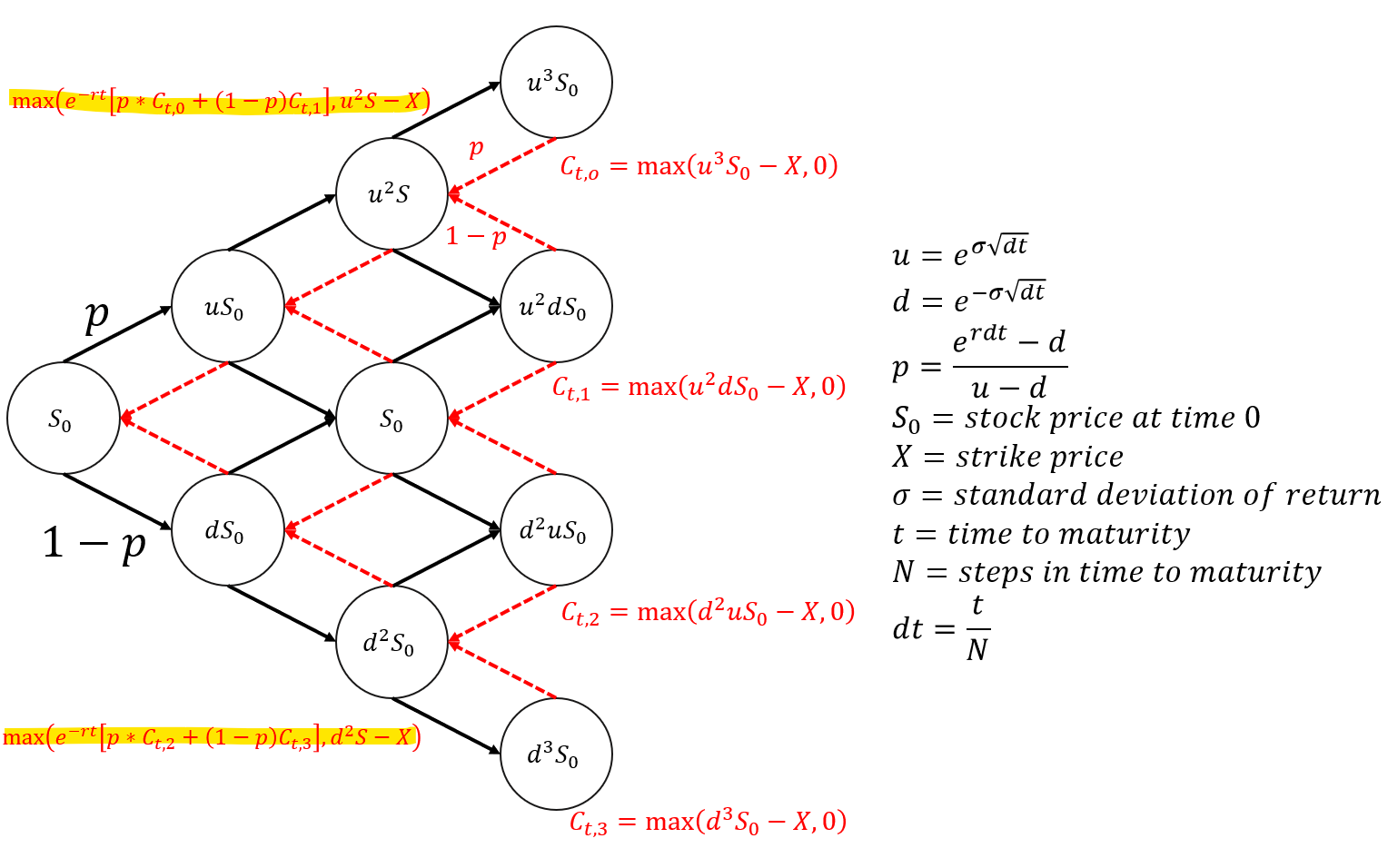
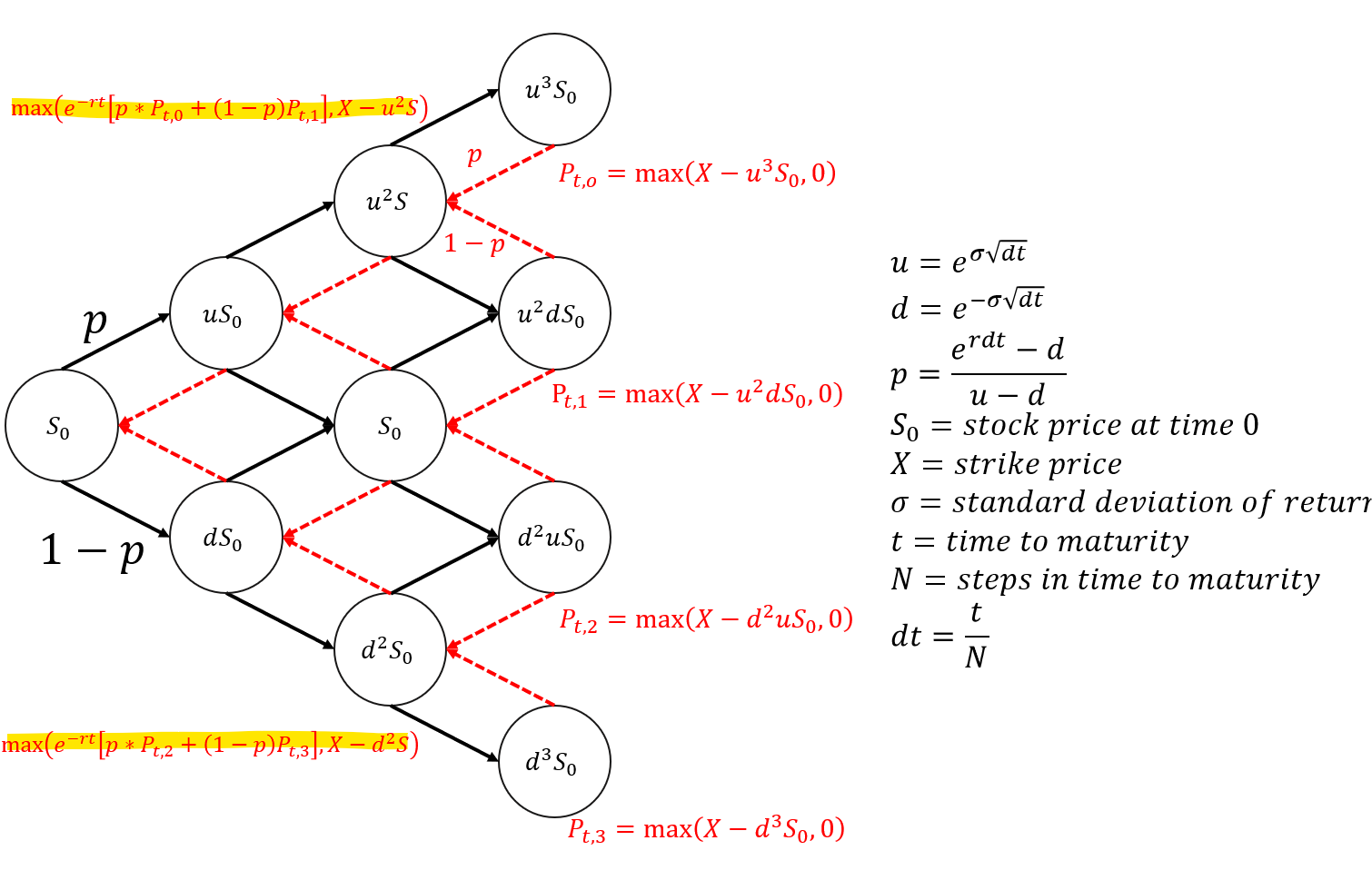
CRR 模型相较于 Black Scholes，可以针对美式买卖权进行订价。所谓的美式选择权就是持有选择权者可以在到期前提前履约，而一般的买卖权则被称为欧式选择权。对于持有人来说，只要当下的内含价值大于回推时的现值时，就有履约动机。因此每个节点的选择权价格会在回推现值与内含价值中取大者，见下图中萤光色部分。

了解 CRR 如何计算选择权价格后，我们直接进入程式化部分。

class crr_model:
    # init fuction
    def __init__(self, s, x, r, t, sigma, N, sigma_daily = True):
        
        t /= 252 
        dt = t/N 
        if sigma_daily:
            sigma *= np.sqrt(252)
        u = np.exp(sigma * math.sqrt(dt))
        d = 1/u
        p = (np.exp(r*dt)-d) / (u-d)
        
        self.s = s
        self.x = x
        self.r = r
        self.t = t
        self.N = N 
        self.dt = dt
        self.u = u
        self.d = d
        self.p = p
        self.sigma = sigma
    
    # european call price
    def eu_call_price(self):
        
        lattice = np.zeros((self.N+1, self.N+1))
        for j in range(self.N+1):
            lattice[self.N, j] = max(0, self.s*(self.u**j)*(self.d**(self.N-j)) - self.x)
        for i in range(self.N-1, -1, -1):
            for j in range(i+1):
                lattice[i, j] = np.exp(-self.r*self.dt)*(self.p*lattice[i+1,j+1] + (1-self.p) * lattice[i+1, j])
    
        return lattice[0,0], lattice
    
    # european put price
    def eu_put_price(self):
        
        lattice = np.zeros((self.N+1, self.N+1))
        for j in range(self.N+1):
            lattice[self.N, j] = max(0, self.x - self.s*(self.u**j)*(self.d**(self.N-j)))
        for i in range(self.N-1, -1, -1):
            for j in range(i+1):
                lattice[i, j] = np.exp(-self.r*self.dt)*(self.p*lattice[i+1,j+1] + (1-self.p) * lattice[i+1, j])
    
        return lattice[0,0], lattice
    
    # american call price
    def am_call_price(self):
        
        lattice = np.zeros((self.N+1, self.N+1))
        for j in range(self.N+1):
            lattice[self.N, j] = max(0, self.s*(self.u**j)*(self.d**(self.N-j)) - self.x)
        for i in range(self.N-1, -1, -1):
            for j in range(i+1):
                lattice[i, j] = max(np.exp(-self.r*self.dt)*(self.p*lattice[i+1,j+1] + (1-self.p) * lattice[i+1, j]),
                                   self.s*(self.u**j)*(self.d**(i-j)) - self.x )
    
        return lattice[0,0], lattice        
    
    # american put price
    def am_put_price(self):

        lattice = np.zeros((self.N+1, self.N+1))
        for j in range(self.N+1):
            lattice[self.N, j] = max(0, self.x - self.s*(self.u**j)*(self.d**(self.N-j)))
        for i in range(self.N-1, -1, -1):
            for j in range(i+1):
                lattice[i, j] = max(
                    np.exp(-self.r*self.dt)*(self.p*lattice[i+1,j+1] + (1-self.p) * lattice[i+1, j]), 
                    self.x - self.s*(self.u**j)*(self.d**(i-j))
                                   )
    
        return lattice[0,0], lattice

为了重现树状结构，我们利用 numpy 的巢状阵列组成一个(N+1)*(N+1)的矩阵，其中最左上角的元素就是选择权的理论价格。其中蓝色线条左下角事实上就是上述的树状图。

s = 100 # set stock price at time 0
x = 95 # set strike price
r = 0 # set risk-free rate = 0%
t = 252 # set time to maturity at 252 days 
sigma = 0.3 # set annualized volatility at 0.3
N = 4 # set steps at 4

crr = crr_model(s, x, r, t, sigma, N, sigma_daily = False)
call, call_lat = crr.eu_call_price()
call_lat

收敛特性

眼尖的读者可能已经注意到变数(N)的存在，N可以视为将到期期间切分成几次，比如: 若到期期间为 252 天， N设定为251 ，表示一天会算一次未来价格，树状图也会有252层。也就是我们的树的层数(N+1)会是由N所决定。问题来了，那N究竟要取多大，才会有更佳的订价结果。事实上，这并没也一个特定的N值，但我们可以发现，随著我们增加N的数量，也就是将时间切得更细碎，计算出来的选择权价格会趋近于一个定值。因此若电脑效能许可之下，N值可以是多多益善的。

# plot the convergency pattern of crr model

calls_ = []
for n in range(1, 100):
    
    s = 100
    x = 100
    r = 0.011
    t = 52
    sigma = 0.3
    
    crr = crr_model(s, x, r, t, sigma, n, sigma_daily = False)
    call, call_lat = crr.eu_call_price()
    calls_.append(call)

plt.plot(range(1, 100), calls_, color = 'red')
plt.xlabel('Numbers of N')
plt.ylabel('Theoretical call price')
plt.title('Options price convergency')
plt.savefig('Options price convergency')
plt.show()

实际案例

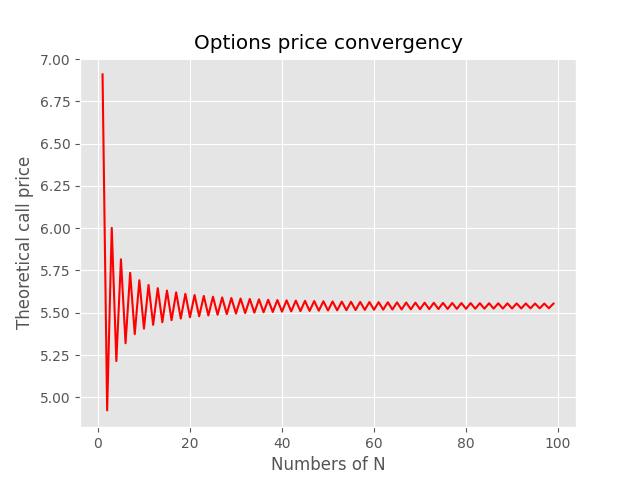
最后我们来观察一下，透过 CRR 模型所得的理论价格与 TEJ 所计算的 Black Scholes 价格以及实际价格进行对比。

我们采用时间为 2023-01-1 到 2023-04-19、履约价格为15500的台指卖权，其中无风险利率采用台湾五年期公债殖利率 — 0.011，Sigma 采用以252天为窗格的台指报酬率标准差，N设定为1000。所得结果如下，可以发现相较于 TEJ 所计算出的 Black Scholes 价格，CRR 价格更接近真实市场价格。

s = stocks.loc['2023-01-31']['close_d'] # get the stock price at the first dat of options trading
x = 15500 # strike price
r = 0.011 # use 5-year Taiwan government bond ytm
t = 51 # time to maturity
sigma = stocks.loc['2023-01-31']['moving volatility'] # get the return volatility at the first day od options trading
N = 100 # divided time 2 maturity into 10 parts

crr = crr_model(s, x, r, t, sigma, N, sigma_daily = True)
call, call_lat = crr.eu_call_price() # european call price
put, put_lat = crr.eu_put_price() # european put price
call_a, call_lat_a = crr.am_call_price() # american call price
put_a, put_lat_a = crr.am_put_price() # american put price

print('CRR theoretical price: ', put)
print('TEJ Black Scholes price: ', puts.loc['2023-01-31']['theoremp'])
print('Real price: ', puts.loc['2023-01-31']['settle'])

结论

CRR 模型作为后起之秀，相较于 Black Scholes 提供了更多的灵活性。之后的衍生性商品热潮中，许多特别的选择权都可使用 CRR 模型或其延伸模型进行订价。其简易的数学计算方法与理论基础，让许多对于选择权投资新手是个入门的好选项。于这篇文章，我们完成了 CRR 模型针对欧式与美式选择权的订价程式化。之后我们会提供更多选择权或衍生性商品相关的知识，欢迎持续关注本平台，此外，也欢迎读者及投资者们选购 TEJ E Shop中的方案来建构自己的选择权定价程式。请注意以上订价公式与选择权商品仅为示范所用，不代表本台任何投资或标的上的建议。

完整程式码

点此前网Github