使用LSTM深度学习模型优化交易讯号,并进行历史回测

目录
文章难度:★★★☆☆
阅读建议:本文使用RNN架构进行时间序列预测,需要对时间序列或是深度学习有基础了解,可以参考前篇LSTM预测股价的文章【资料科学】LSTM,有助于对本文有更深入的了解。
上篇我们选用了 LSTM 模型来进行股价走势的预测,使用前10天的开盘价、最高价、最低价、收盘价、成交量,预测隔天的收盘价,发现模型表现不是很好,仅仅以昨天的股价来对明天股价进行预测,因此我们更改个做法,想借由模型来帮我们判断卖卖点,进行交易策略。这次我们更增加了更多特征指标,希望能有更好的结果。
我们新增了八种特征指标,四种为技术指标,四种为总经指标,希望能用这两个面向的特征值提升我们的预测结果。
技术指标:
KD:随机指标,表示目前价格相对过去一段期间的高低变化。
RSI:股价强弱指标,表示买卖盘双方力道的强弱。
MACD:长期与短期移动平均线收敛或发散指标。
MOM:主要是用来观察价格走势的变化幅度,以及行情的趋动方向。总经指标:
台湾景气对策信号:代表经济活动且能反映景气变化的重要总体经济变数。
VIX指数:表示市场波动度外,也是市场情绪恐慌指标。
领先指标:提前反应景气的经济指标,用来预测未来景气走向。
台股平均本益比:以上市公司取平均,可看出整体投资人对整个市场的看法是乐观还是悲观。
本文使用Windows OS并以Jupyter作为编辑器
import tejapi
import pandas as pd
tejapi.ApiConfig.api_key = "Your Key"
tejapi.ApiConfig.ignoretz = True
0050调整股价(日) — 除权息调整(TWN/APRCD1)
台股平均本益比 — 总体经济(GLOBAL/ANMAR)
台湾景气对策讯号– 总体经济(GLOBAL/ANMAR)
领先指标 — 总体经济(GLOBAL/ANMAR)
芝加哥VIX指数 — 国际股价指数(GLOBAL/GIDX)
0050除权息调整股价与其开盘价、收盘价、最高价、最低价、成交量,资料期间2011年1月至2022年11月。
coid = "0050"
mdate = {'gte':'2011-01-01', 'lte':'2022-11-15'}
data = tejapi.get('TWN/APRCD1',
coid = coid,
mdate = {'gte':'2011-01-01', 'lte':'2022-11-15'},
paginate=True)
#开高低收、成交量
data = data[["coid","mdate","open_adj","high_adj","low_adj","close_adj","amount"]]
data = data.rename(columns={"coid":"coid","mdate":"mdate","open_adj":"open",
"high_adj":"high","low_adj":"low","close_adj":"close","amount":"vol"})
技术指标(KD、RSI、MACD、MOM)
from talib import abstract
data["rsi"] = abstract.RSI(data,timeperiod=14)
data[["macd","macdsig","macdhist"]] = abstract.MACD(data)
data[["kdf","kds"]] = abstract.STOCH(data)
data["mom"] = abstract.MOM(data,timeperiod=15)
data.set_index(data["mdate"],inplace = True)
总经指标(台股平均本益比、台湾景气对策讯号、领先指标、芝加哥VIX指数)
data1 = tejapi.get('GLOBAL/ANMAR',
mdate = mdate,
coid = "SA15",
paginate=True)
data1.set_index(data1["mdate"],inplace = True)
data1 = data1.resample('D').ffill()
data = pd.merge(data,data1["val"],how='left', left_index=True, right_index=True)
data.rename({"val":"pe"}, axis=1, inplace=True)
#芝加哥VIX指数
data2 = tejapi.get('GLOBAL/GIDX',
coid = "SB82",
mdate = mdate,
paginate=True)
data2.set_index(data2["mdate"],inplace = True)
data = pd.merge(data,data2["val"],how='left', left_index=True, right_index=True)
data.rename({"val":"vix"}, axis=1, inplace=True)
#景气对策讯号
data3 = tejapi.get('GLOBAL/ANMAR',
coid = "EA1101",
mdate = mdate,
paginate=True)
data3.set_index(data3["mdate"],inplace = True)
data3 = data3.resample('D').ffill()
data = pd.merge(data,data3["val"],how='left', left_index=True, right_index=True)
data.rename({"val":"light"}, axis=1, inplace=True)
#领先指标
data4 = tejapi.get('GLOBAL/ANMAR',
coid = "EB0101",
mdate = mdate,
paginate=True)
data4.set_index(data4["mdate"],inplace = True)
data4 = data4.resample('D').ffill()
data = pd.merge(data,data4["val"],how='left', left_index=True, right_index=True)
data.rename({"val":"advance"}, axis=1, inplace=True)
删除空值与无用栏位
data.set_index(data["mdate"],inplace=True)
data = data.fillna(method="pad",axis=0)
data = data.dropna(axis=0)
del data["coid"]
del data["mdate"]
data
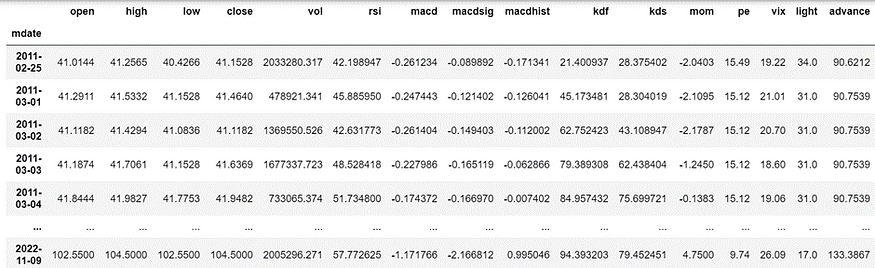
我们选用移动平均结合动能指标来定义趋势,简单运用MA10 > MA20 且 RSI10 >RSI 20时,判断为上升趋势。
data["short_mom"] = data["rsi"].rolling(window=10,min_periods=1,center=False).mean()
data["long_mom"] = data["rsi"].rolling(window=20,min_periods=1,center=False).mean()
data["short_mov"] = data["close"].rolling(window=10,min_periods=1,center=False).mean()
data["long_mov"] = data["close"].rolling(window=20,min_periods=1,center=False).mean()
标记Labels
上升趋势标的为1,反之标记为0
import numpy as np
data['label'] = np.where(data.short_mov > data.long_mov, 1, 0)
data = data.drop(columns=["short_mov"])
data = data.drop(columns=["long_mov"])
data = data.drop(columns=["short_mom"])
data = data.drop(columns=["long_mom"])
观察资料分布情形
可见资料分布不无过度不均,但由于大盘整体趋势向上,上升趋势较多为正常现象。
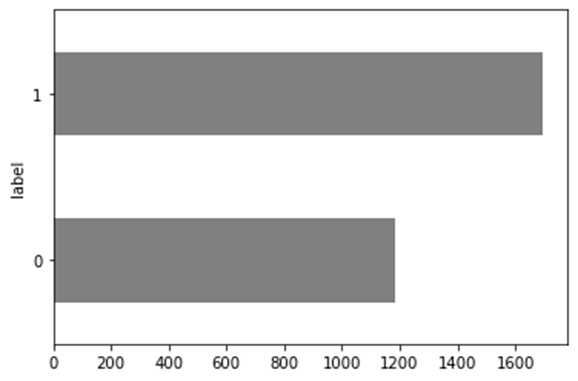
资料标准化
X = data.drop('label', axis = 1)
from sklearn.preprocessing import StandardScaler
X[X.columns] = StandardScaler().fit_transform(X[X.columns])
y = pd.DataFrame({"label":data.label})
切割成学习样本以及测试样本,比例为7:3
训练资料时间范围为2011.02.25–2019.05.08
测试资料时间范围为2019.05.09–2022.11.15
import numpy as np
split = int(len(data)*0.7)
train_X = X.iloc[:split,:].copy()
test_X = X.iloc[split:].copy()
train_y = y.iloc[:split,:].copy()
test_y = y.iloc[split:].copy()
X_train, y_train, X_test, y_test = np.array(train_X), np.array(train_y), np.array(test_X), np.array(test_y)
将资料维度改成三维符合接下来模型所需
X_train = np.reshape(X_train, (X_train.shape[0],1,16))
y_train = np.reshape(y_train, (y_train.shape[0],1,1))
X_test = np.reshape(X_test, (X_test.shape[0],1,16))
y_test = np.reshape(y_test, (X_test.shape[0],1,1))
加入模型
加入四层LSTM 层,并以 Dropout 防止过拟
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import LSTM
from keras.layers import Dropout
from keras.layers import BatchNormalization
regressor = Sequential()
regressor.add(LSTM(units = 32, return_sequences = True, input_shape = (X_train.shape[1], X_train.shape[2])))
regressor.add(BatchNormalization())
regressor.add(Dropout(0.35))
regressor.add(LSTM(units = 32, return_sequences = True))
regressor.add(Dropout(0.35))
regressor.add(LSTM(units = 32, return_sequences = True))
regressor.add(Dropout(0.35))
regressor.add(LSTM(units = 32))
regressor.add(Dropout(0.35))
regressor.add(Dense(units = 1,activation="sigmoid"))
regressor.compile(optimizer = 'adam', loss="binary_crossentropy",metrics=["accuracy"])
regressor.summary()


将epochs 设定为100次。
train_history = regressor.fit(X_train,y_train,
batch_size=200,
epochs=100,verbose=2,
validation_split=0.2)

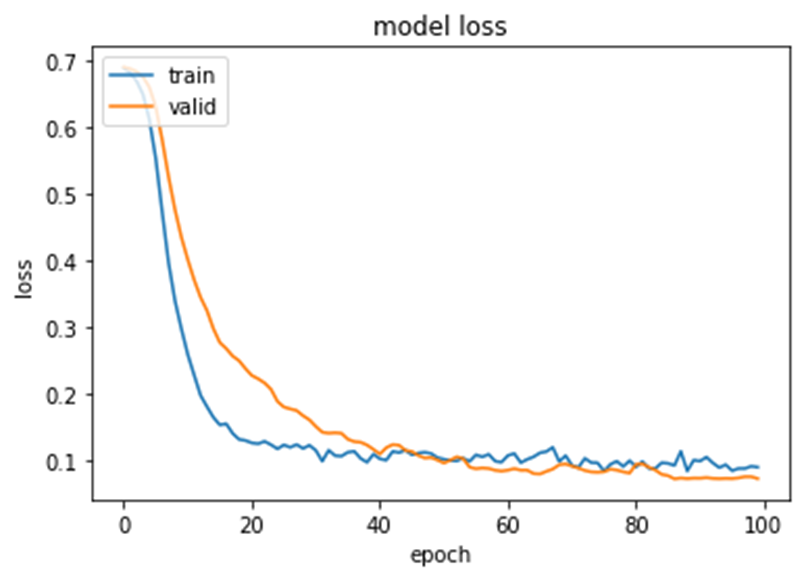
藉Model loss 图可看出训练过程中两条线有收敛情形,显示模型无过拟合。
import matplotlib.pyplot as plt
loss = train_history.history["loss"]
var_loss = train_history.history["val_loss"]
plt.plot(loss,label="loss")
plt.plot(var_loss,label="val_loss")
plt.ylabel("loss")
plt.xlabel("epoch")
plt.title("model loss")
plt.legend(["train","valid"],loc = "upper left")
可看出不同特征值的重要程度为何。显示MACD、台股平均本益比及RSI为重要特征值。
from tqdm.notebook import tqdm
results = []
print(' Computing LSTM feature importance...')
# COMPUTE BASELINE (NO SHUFFLE)
oof_preds = regressor.predict(X_test, verbose=0).squeeze()
baseline_mae = np.mean(np.abs(oof_preds-y_test))
results.append({'feature':'BASELINE','mae':baseline_mae})
for k in tqdm(range(len(list(test_X.columns)))):
# SHUFFLE FEATURE K
save_col = X_test[:,:,k].copy()
np.random.shuffle(X_test[:,:,k])
# COMPUTE OOF MAE WITH FEATURE K SHUFFLED
oof_preds = regressor.predict(X_test, verbose=0).squeeze()
mae = np.mean(np.abs( oof_preds-y_test ))
results.append({'feature':test_X.columns[k],'mae':mae})
X_test[:,:,k] = save_col

测试集准确率高达 95.49%,显示LSTM 模型能不错的执行我们的策略。
regressor.evaluate(X_test, y_test,verbose=1)
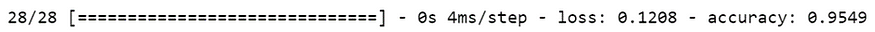
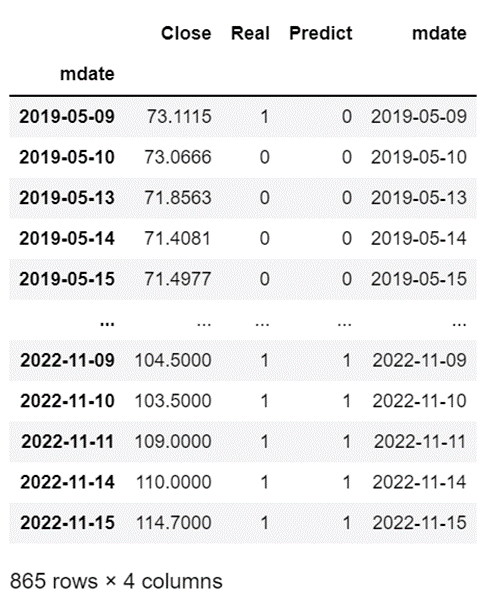
将真实 (Real) Label与模型预测 (Predict) Label进行对照
LSTM策略预测趋势表示图,红色代表上升趋势,绿色代表下降趋势。
import matplotlib.pyplot as plt
import matplotlib.dates as mdates
import datetime as dt
df = result.copy()
df = df.resample('D').ffill()
t = mdates.drange(df.index[0], df.index[-1], dt.timedelta(hours = 24))
y = np.array(df.Close[:-1])
fig, ax = plt.subplots()
ax.plot_date(t, y, 'b-', color = 'black')
for i in range(len(df)):
if df.Predict[i] == 1:
ax.axvspan(
mdates.datestr2num(df.index[i].strftime('%Y-%m-%d')) - 0.5,
mdates.datestr2num(df.index[i].strftime('%Y-%m-%d')) + 0.5,
facecolor = 'red', edgecolor = 'none', alpha = 0.5
)
else:
ax.axvspan(
mdates.datestr2num(df.index[i].strftime('%Y-%m-%d')) - 0.5,
mdates.datestr2num(df.index[i].strftime('%Y-%m-%d')) + 0.5,
facecolor = 'green', edgecolor = 'none', alpha = 0.5
)
fig.autofmt_xdate()
fig.set_size_inches(20,10.5)
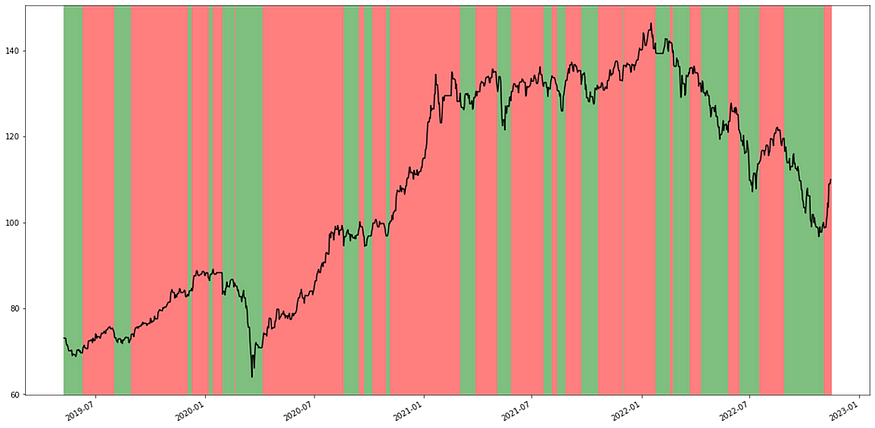
当趋势讯号为上升时买入一部位并持有,当趋势讯号为下降时卖出原部位,并反手做空一部位并持有,直到下次讯号为上升趋势时平仓。
*注:本策略不考虑手续费,且均为全部资金进场与出场。
test_data = data.iloc[split:].copy()
backtest = pd.DataFrame(index=result.index)
backtest["r_signal"] = list(test_data["label"])
backtest["p_signal"] = list(result["Predict"])
backtest["m_return"] = list(test_data["close"].pct_change())
backtest["r_signal"] = backtest["r_signal"].replace(0,-1)
backtest["p_signal"] = backtest["p_signal"].replace(0,-1)
backtest["a_return"] = backtest["m_return"]*backtest["r_signal"].shift(1)
backtest["s_return"] = backtest["m_return"]*backtest["p_signal"].shift(1)
backtest[["m_return","s_return","a_return"]].cumsum().hist()
backtest[["m_return","s_return","a_return"]].cumsum().plot()

LSTM 策略累积报酬为82.6%
实际策略(MA+MOM)累积报酬为71.3%
大盘Buy and Hold累积报酬为52%
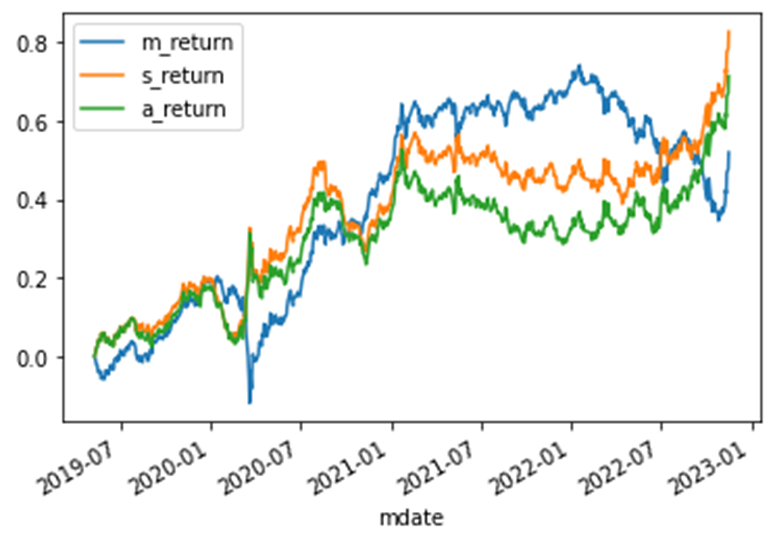
此次主要的重点在于 LSTM 是否可以依照我们设定的原策略,正确的判断出买卖点。结果是肯定的,并拥有 95.49% 的高准确率,回测结果累积报酬 82.6% 甚至是赢过原策略并显著打败大盘的52%,我们认为打败原策略的原因在于在盘整期间 LSTM 产生了较少的交易讯号,避免了原策略盘整期间容易上下刷洗,导致交易绩效下降的情形。
最后,还是要再次提醒本文所提及之标的仅供说明使用,不代表任何金融商品之推荐或建议。因此,若读者对于建置策略、绩效回测、研究实证等相关议题有兴趣,欢迎选购 TEJ E Shop中的方案,具有齐全的资料库,就能轻易的完成各种检定。

电子报订阅