使用PCA主成份分析优化投资组合
目录
文章难度:★★★★☆
数学的本质不是将简单的事情变复杂,而是将复杂的事物简化。- Stan Gudder
主成分分析(Principal Component Analysis,后简称为 PCA),为非监督式学习中的一项关键技术,被广泛用于机器学习与统计学领域来分析资料、降低数据维度。核心精神在于将原始数据拆解成具有代表性的主成分,达到降维的目的,并重新描述数据。
本研究的主旨在于运用股票的日报酬资料,利用 PCA 来取得主成分,并建立投资组合。阅读本篇文章读者将会看到以下重点:
了解 PCA 之特征值与特征向量,并以此设计投资组合
回测投资组合绩效的方法,可用于各式投资策略
本文使用Windows OS并以jupyter作为编辑器
import tejapi
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
tejapi.ApiConfig.api_key = "Your Key"
0050指数成分股资料集 — 上市上柜指数(TWN/EWISAMPLE)
0050股价报酬(日)-报酬率(TWN/APRCD2)
0050调整股价(日) — 除权息调整(TWN/APRCD1)
指数资料期间:2013.01.01–2022.11.24
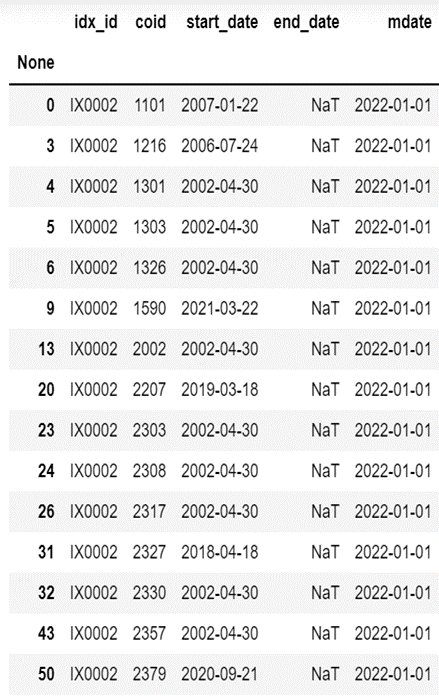
0050成分股载入,载入规则依照[“end_date”]栏位做筛选,选出目前尚在成分股中的股票。
mdate = {'gte':'2000-01-01', 'lte':'2022-11-24'}
data = tejapi.get('TWN/EWISAMPLE',
idx_id = "IX0002",
start_date = mdate,
paginate=True)
data1 = data[data["end_date"] < "2022-11-24"]
diff_data = pd.concat([data,data1,data1]).drop_duplicates(keep=False)
coid = list(diff_data["coid"])
print(len(coid))
diff_data
0050报酬率载入
for i in range(0,len(coid)):
print(i)
if i == 0:
df = tejapi.get('TWN/EWPRCD2',
coid = coid[i],
mdate = {'gte':'2013-01-01', 'lte':'2022-11-24'},
paginate=True)
df.set_index(df["mdate"],inplace=True)
Df = pd.DataFrame({coid[i]:df["roia"]})
else:
df = tejapi.get('TWN/EWPRCD2',
coid = coid[i],
mdate = {'gte':'2013-01-01', 'lte':'2022-11-24'},
paginate=True)
df.set_index(df["mdate"],inplace=True)
Df1 = pd.DataFrame({coid[i]:df["roia"]})
Df = pd.merge(Df,Df1[coid[i]],how='left', left_index=True, right_index=True)
日月光投控( 3711 )于 2018/04/30 后上市才有报酬率资料,予以剔除。
上海商业储蓄银行( 5876 )于 2014/09/25 后上市才有报酬率资料,予以剔除。
矽力-KY (6415)于 2013–12–12 后上市才有报酬率资料,予以剔除。
del Df["3711"]
del Df["5876"]
del Df["6415"]
故本文改以截至 2022/11/24 前,0050成分股并剔除以上3档股票,共 47 档为研究对象。
故本文改以截至 2022/11/24 前,0050成分股并剔除以上3档股票,共 47 档为研究对象。
资料视觉化
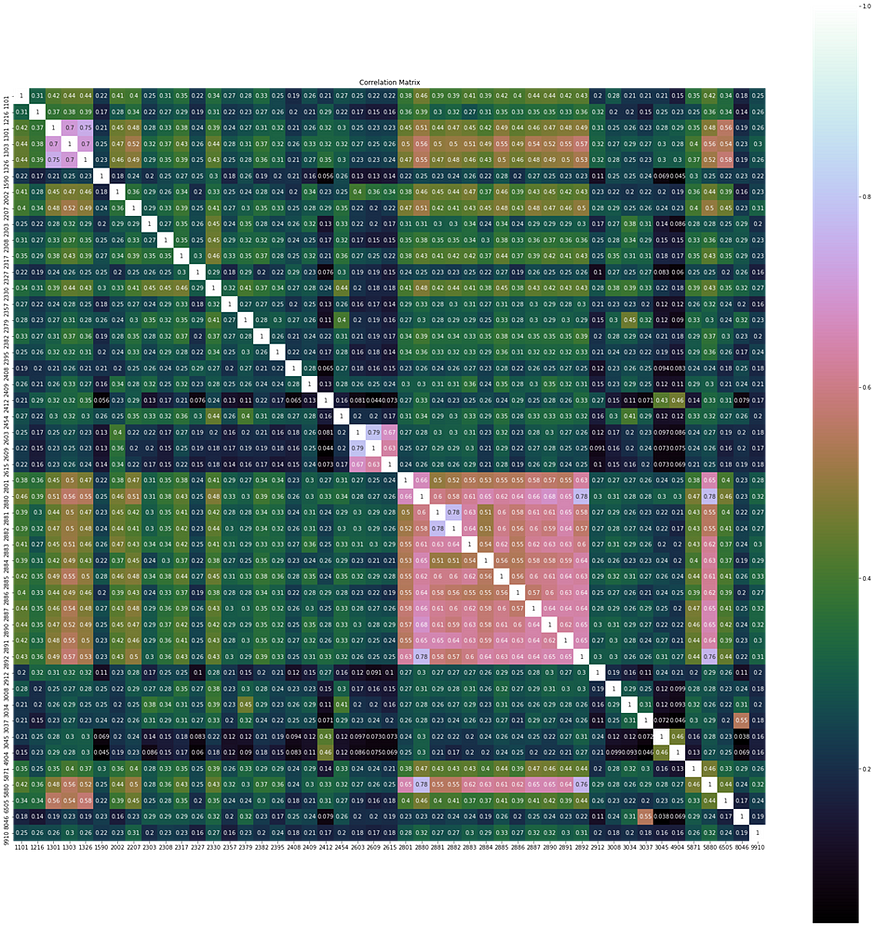
首先我们须对资料集有基本的认识,我们观察各成本股报酬率的相关性,可以看出日报酬间存在显著正相关性,因此资料可以更低的维度来表达,即小于目前的 47 维度。
cor = Df.corr()
plt.figure(figsize=(30,30))
plt.title("Correlation Matrix")
sns.heatmap(cor, vmax=1,square=True,annot=True,cmap="cubehelix")
资料标准化
建模型之前,我们并不知道资料集中每个特征的重要性,这很可能造成大量信息流失,因此对每个特征进行标准化处理,使得资料范围相同,再进行PCA。
scale = StandardScaler().fit(Df)
rescale = pd.DataFrame(scale.fit_transform(Df),columns=Df.columns,index=Df.index)
#标准化视觉化
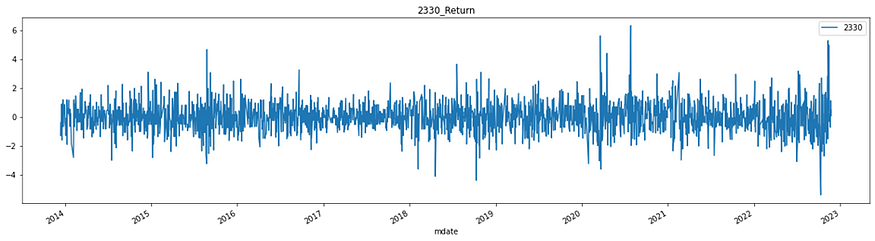
plt.figure(figsize=(20,5))
plt.title("2330_Return")
rescale["2330"].plot()
plt.grid=True
plt.legend()
plt.show()
模型设置
我们希望将原有的 47 维度资料降低至 10 维度,让原始资料以10个主成分来表示即可。
n_components = 10
pca = PCA(n_components=n_components)
Pc = pca.fit(X_train)
PCA 解释变数
第一主成分表示了原始资料中最大的变异数,第二个主成分表示了原始资料中的第二大变异数,并以次类推。
fig, axes = plt.subplots(ncols=2)
Series1 = pd.Series(Pc.explained_variance_ratio_[:n_components ]).sort_values()
Series2 = pd.Series(Pc.explained_variance_ratio_[:n_components ]).cumsum()
Series1.plot.barh(title="Explained Variance",ax=axes[0])
Series2.plot(ylim=(0,1),ax=axes[1],title="Cumulative Explained Variance")
print("变数累积解释比例:")
print(Series2[len(Series2)-1:len(Series2)].values[0])
print("各变数解释比例:")
print(Series1.sort_values(ascending=False))
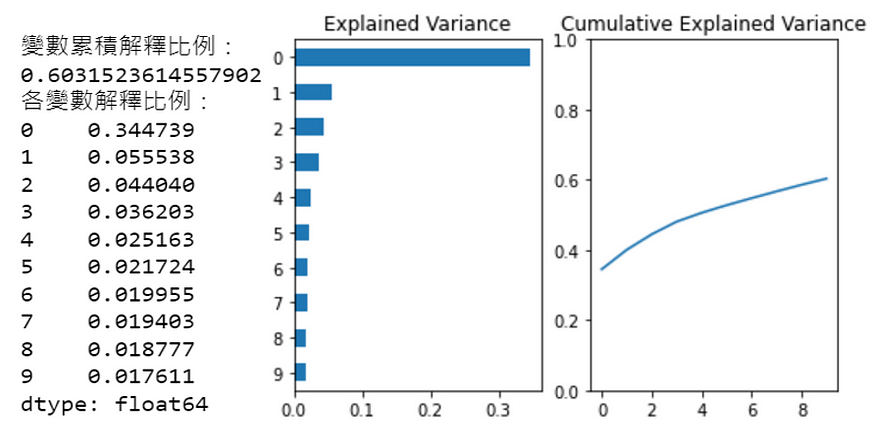
由左图可看出前 10 个主成分解释变异数情形,第一个主成分就占了原资料35% 的变异数,代表第一主成分解释了 35% 的 47 档股票日报酬变化,而这个决定性很大的主成分通常称作「市场」因素。
由右图可看出前 10个主成分,共解释了这 47 档股票日报酬约 60% 的变异数。
设置投资组合权重
在上个步骤中,我们看出主成分解释变数情形,接下来探讨原先资料,也就是 47 档股票,对这 10 个主成分的相关性。并以此设计投资组合权重。
n_components = 10
weights = pd.DataFrame()
for i in range(n_components):
weights["weights_{}".format(i)] = pca.components_[i] / sum(pca.components_[i])
weights = weights.values.T
weight_port = pd.DataFrame(weights,columns=Df.columns)
weight_port.index = [f'Portfolio{i}' for i in range(weight_port.shape[0])]
weight_port
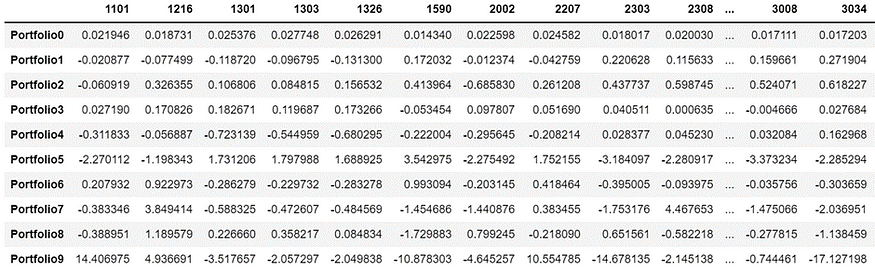
解释投资组合权重设置方法
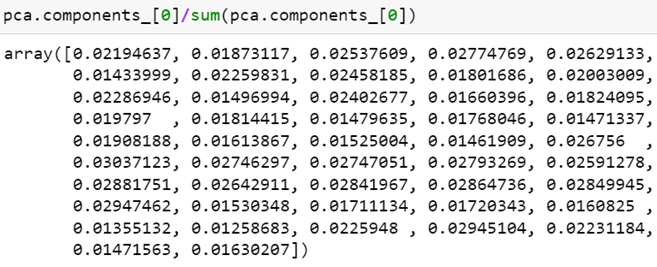
第一主成分解释了 35% 的变异,我们来看各变数(47档股票),对第一主成分的相关性。
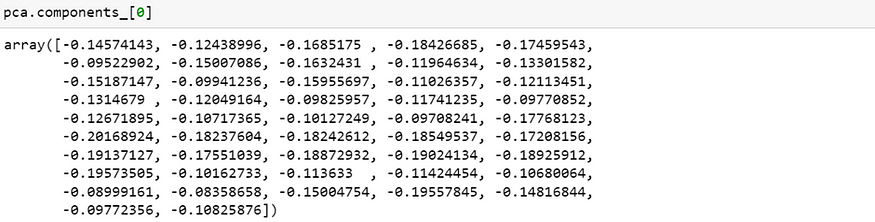
由 array 中可看出,47 档股票对于第一主成分的相关性都是同向的(均为负数),而数值大小差异并不大,这更可以验证我们上述说明第一主成分为「市场」因素。
weight_port.iloc[0].T.sort_values(ascending=False).plot.bar(subplots=True,figsize=(20,5),
legend=False,sharey=True,ylim=(-0.75,0.75))
再来,我们以各股票的相关性 / 各股票相关性数值总和 ,完成投资组合权重。
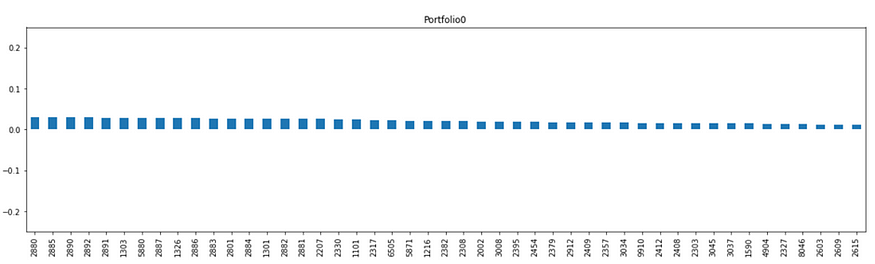
画出前五大主成分投资组合之权重
weight_port[:5].T.plot.bar(subplots=True,layout = (int(5),1),figsize=(20,25),
legend=False,sharey=True,ylim=(-2,2))
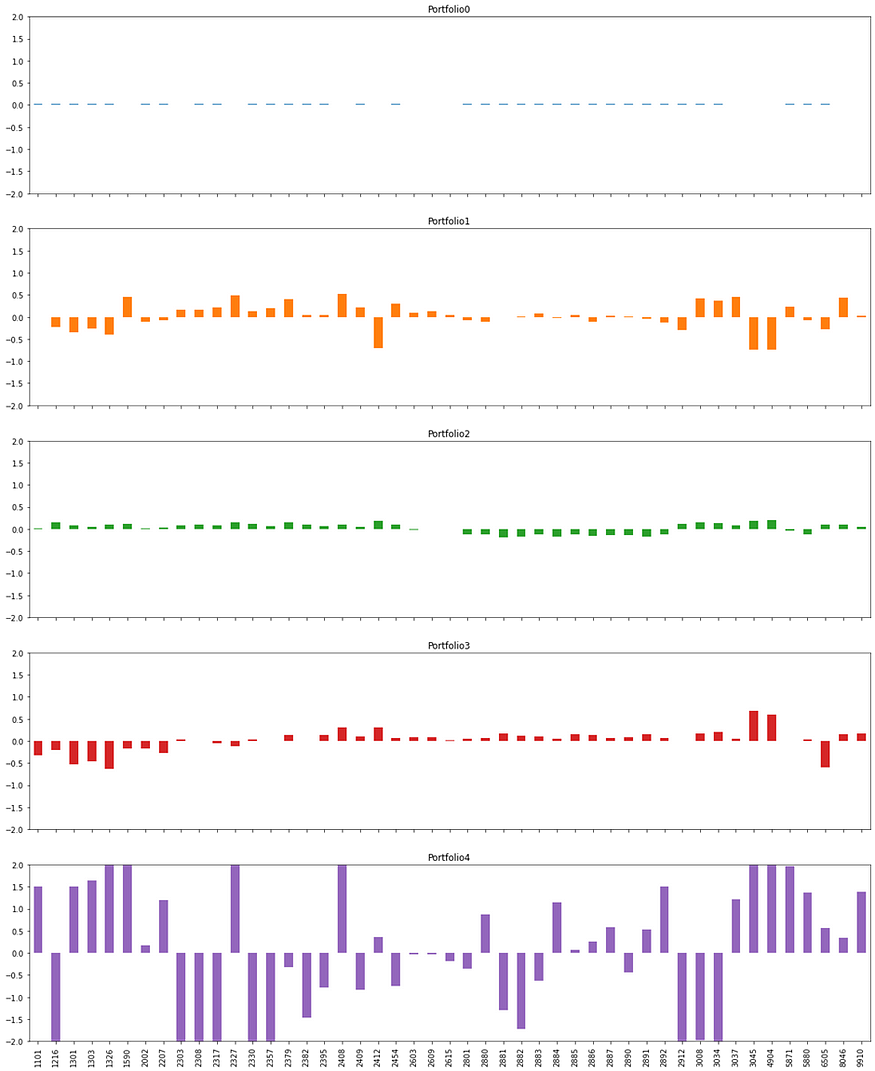
检视其他主成分分类逻辑
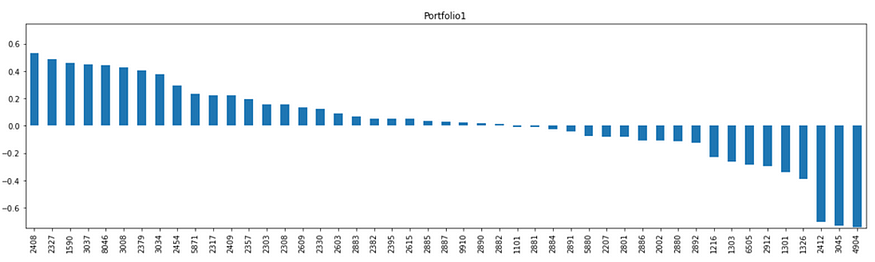
Portfolio 1
前三名分别为南亚科(2408)、国巨(2327)、亚德克KY(1590);后三名分别为远传(4904)、台湾大(3045)、中华电(2412),可看出Portfolio 1电子股权重较高,传产、电信股较低。
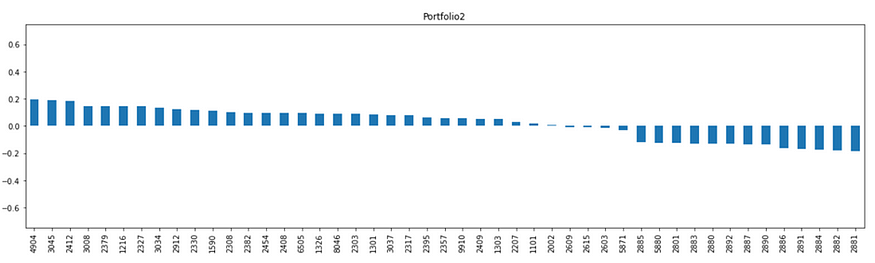
Portfolio 2
前三名反而为电信三雄,而后面大多为金融股,可看出Portfolio 2为非金融投资组合。
我们以夏普比率( Sharpe Ratio )来做为衡量指标,夏普率(或夏普值)是在基金投资或是资产配置时,用来衡量整个投资组合绩效与稳定性的重要指标。表示「在承受1%的风险下,能得到多少报酬?」
本文夏普比率公式 = 以年化报酬率 / 年化风险做计算
def sharpe_ratio(ts_returns):
ts_returns = ts_returns
days = ts_returns.shape[0]
n_years = days/252
if ts_returns.cumsum()[-1] < 0:
annualized_return = (np.power(1+abs(ts_returns.cumsum()[-1])*0.01,1/n_years)-1)*(-1)
else:
annualized_return = np.power(1+abs(ts_returns.cumsum()[-1])*0.01,1/n_years)-1
annualized_vol = (ts_returns*0.01).std()*np.sqrt(252)
annualized_sharpe = annualized_return / annualized_vol
return annualized_return,annualized_vol,annualized_sharpe
选出Top5 Portfolio
n_components = 10
annualized_ret = np.array([0.]*n_components)
sharpe_metric = np.array([0.]*n_components)
annualized_vol = np.array([0.]*n_components)
coids = X_train.columns.values
n_coids = len(coids)
pca = PCA(n_components=n_components)
Pc = pca.fit(X_train)
pcs = pca.components_
for i in range(n_components):
pc_w = pcs[i] / sum(pcs[i])
eigen_port = pd.DataFrame(data={"weights":pc_w.squeeze()},index=coids)
eigen_port.sort_values(by=["weights"],ascending=False,inplace=True)
#权重与每天报酬内积,得出每日投资组合报酬
eigen_port_returns = np.dot(X_train.loc[:,eigen_port.index],eigen_port["weights"])
eigen_port_returns = pd.Series(eigen_port_returns.squeeze(),
index = X_train.index)
ar,vol,sharpe = sharpe_ratio(eigen_port_returns)
annualized_ret[i] = ar
annualized_vol[i] = vol
sharpe_metric[i] = sharpe
sharpe_metric = np.nan_to_num(sharpe_metric)
N=5
result = pd.DataFrame({"Annual Return":annualized_ret,"Vol":annualized_vol,"Sharpe":sharpe_metric})
result.dropna(inplace=True)
#Sharpe Ratio of PCA portfolio
ax = result[:N]["Sharpe"].plot(linewidth=3,xticks=range(0,N,1))
ax.set_ylabel("Sharpe")
result.sort_values(by=["Sharpe"],ascending=False,inplace=True)
print(result[:N])

画出投资组合期间报酬走势图
def Backtest(i,data):
pca = PCA()
Pc = pca.fit(data)
pcs = pca.components_
pc_w = pcs[i] / sum(pcs[i])
eigen_port = pd.DataFrame(data={"weights":pc_w.squeeze()},index=coids)
eigen_port.sort_values(by=["weights"],ascending=False,inplace=True)
#权重与每天报酬取内积得出每日投资组合报酬
eigen_port_returns = np.dot(data.loc[:,eigen_port.index],eigen_port["weights"])
eigen_port_returns = pd.Series(eigen_port_returns.squeeze(),
index = data.index)
ar,vol,sharpe = sharpe_ratio(eigen_port_returns)
return eigen_port_returns,ar,vol,sharpe
报酬走势视觉化
def Weight_plot(i):
top_port = weight_port.iloc[[i]].T
port_name = top_port.columns.values.tolist()
top_port.sort_values(by=port_name,ascending=False,inplace=True)
ax = top_port.plot(title = port_name[0],xticks=range(0,len(coids),1),
figsize=(15,6),
rot=45,linewidth=3)
ax.set_ylabel("Portfolio Weight")
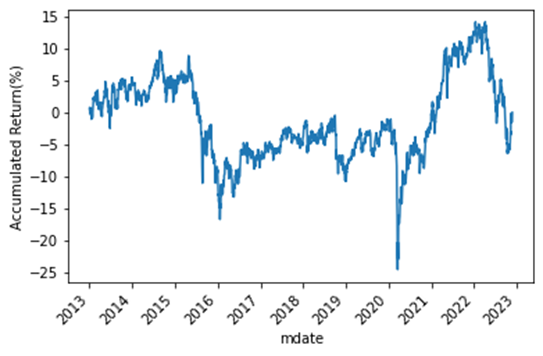
portfolio = 0
train_returns,train_ar,train_vol,train_sharpe = Backtest(portfolio,X_train)
ax = train_returns.cumsum().plot(rot=45)
ax.set_ylabel("Accumulated Return(%)")
Weight_plot(portfolio)
小结
以上提供投资组合简单的回测方法并视觉化,可见由 PCA 方法建构的投资组合绩效并不好,其实这也是可预见的,PCA 只是针对报酬相关性做投组分类,并不代表能有好的报酬。
本篇提供 PCA 针对台湾 50指数(因资料缺失剔除三档),共 47 档股票,针对日报酬做研究,将原 47 档股票降维成 10个主成分,根据主成分与各股票之相关性,建构投组权重并针对各别主成分做讨论,除了可看出股票市场中影响最大的「市场」因素确实存在,也可看出 PCA 在分类方面仍有一定逻辑。惟要详细解释每个主成分所代表的意义然有其困难所在。
最后,还是要再次提醒本文所提及之标的仅供说明使用,不代表任何金融商品之推荐或建议。因此,若读者对于建置策略、绩效回测、研究实证等相关议题有兴趣,欢迎选购 TEJ E Shop中的方案,具有齐全的资料库,就能轻易的完成各种检定。

电子报订阅